05. Block Ciphers

Main bulk encryption algorithms used in commercial applications. AES is one example of such algorithm.

Principles

Block ciphers are symmetric key ciphers where each block of plaintext encrypted with the same key.

A block is a set of plaintext symbols of a fixed size, typically 64 to 256 bits in modern ciphers.

They are used in configurations called modes of operation.

Notation

• $P$: plaintext block of length $n$ bits
• $C$: ciphertext block of length $n$ bits
• $K$: key of length $k$ bits
• Encryption: $C = E(P, K)$
• Decryption: $P = D(C, K)$

Criteria

Shannon defined two encryption techniques:

• Confusion: substitution used to make the relationship between $K$ and $C$ as complex as possible.
• Diffusion: transformations used to dissipate the statistical properties of $P$ across $C$.

Repeated use of techniques can be used using the concept of a product cipher.

Product & Iterated Ciphers

Product Cipher

Cryptosystem where encryption performed by applying/composing several sub-encryption algorithms: output of one block used as input to next block.

Often composed of simple functions $f_i$ for $1 \le i \le r$ such that each $f_i$ has its own key $K_i$.

Iterated Cipher

Special product ciphers called iterated ciphers where:

• Encryption divided into $r$ similar rounds
• Sub-encryption functions are the same function $g$: the round function
• Each round key/subkey $K_i$ is derived from the master key $K$ using a process called key schedule

Encryption

Given plaintext block $P$, round function $g$, round keys $K-1, K_2, \dots, K_r$, the ciphertext block $C$ is derived through $r$ rounds:

Decryption

There must be an inverse function $g^{-1}$ such that $g^{-1}(g(W, K_i), K_i) = W$ for all keys $K_i$ and blocks $W$.

Types of Iterated Ciphers

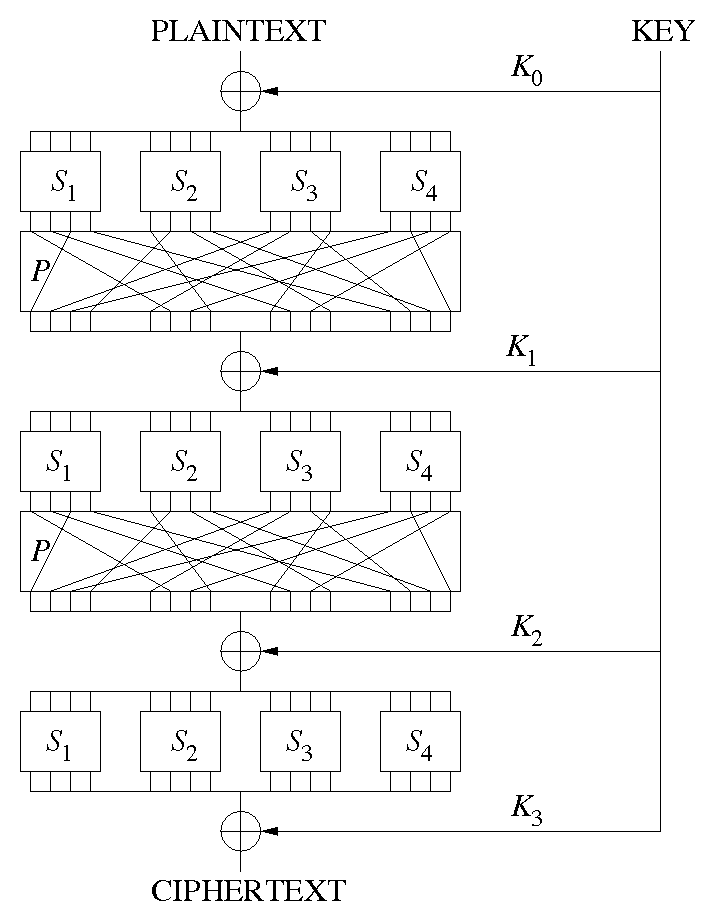
Substitution-Permutation Network (SPN) e.g. Advanced Encryption Standard (AES).

Feistel Cipher e.g. Data Encryption Standard (DES).

Substitution-Permutation Network

Block length $n$ must allow each block to be split into $m$ sub-blocks of length $l$: $n = lm$.

Substitution $\pi_S$ (called substitution box or S-box) operates on sub-blocks of length $l$ bits:

i.e. mapping some binary number of size $l$ bits to another.

Permutation $\pi_P$ (called permutation-box or P-box) swaps the inputs from $\{ 1, \dots, n \}$:

i.e. swapping the order of bits in the entire block around.

Operation

1. Round key $K_i$ XORed with current state block $W_i$: $K_i \oplus W_i$
2. Each sub-block substituted applying $\pi_S$
3. The whole block permuted using $\pi_P$

Example

• 4 round keys
• 4 S-boxes
• 1 P-box
• Last round does have a P-block

Feistel Cipher

Round function swaps the two halves of the block to form a new right hand half.

Encryption

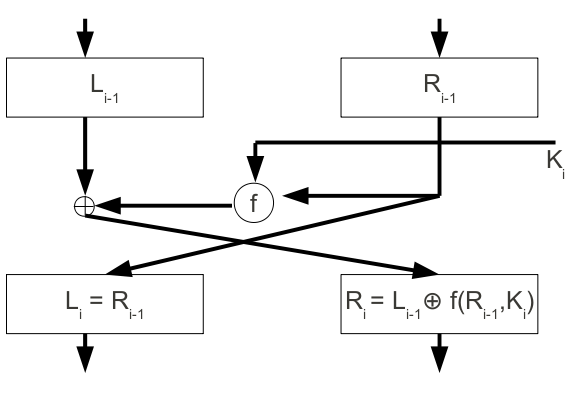
Plaintext block $P = W_0$ split into two halves $(L_0, R_0)$.

For each round:

• $L_i = R_{i - 1}$
• $R_i = L_{i - 1} \oplus f(R_{i - 1}, K_i)$

The output is the ciphertext block $C = W_R = (L_r, R_r)$.

Decryption

Split $C$ into two halves, $(L_r, R_r)$.

For each round:

• $L_{i - 1} = R_i \oplus f(L_i, K_i)$
• $R_{i - 1} = L_i$

$f$ does not need to be inverted: $x \oplus x = 0$, so applying by applying $f$ twice it can be decrypted.

The choice of $f$ is critical for security; is is the only non-linear part of the encryption.

Differential and Linear Cryptanalysis

Differential cryptanalysis: chosen plaintext attack using correlation in the differences between two input plaintexts and their corresponding ciphertexts.

Liner cryptanalysis: known plaintext attack that theoretically break DES.

Modern block ciphers normally immune to both attacks.

Avalanche Effects

Key avalanche: a small change in key (with the same plaintext) should result in a large change in ciphertext.

Plaintext avalanche: a small change in plaintext should result in a large change in ciphertext: changing one bit should change all bits in the ciphertext with a probability of $1/2$.

Key avalanche is related to Shannon’s notion of confusion, plaintext avalanche to Shannon’s notion of diffusion.

DES

Designed by IBM researchers, became US standard in 1976. 16-round Feistel cipher with key length of 56 bits and data block length of 64 bits.

The key length is actually 64 bits, but the last bit of every byte is redundant.

Encryption

$P$ is an input plaintext block of 64 bits:

1. All bits of $P$ permuted using an initial fixed permutation of $IP$
2. 16 rounds of Feistel operations applied, denoted by function $f$
   • Each round uses a different 48-bit subkey
   • The subkey is defined by a series of permutations and shifts
3. A final fixed inverse permutation $IP^{-1}$ is applied

The 64-bit ciphertext block $C$ is the output.

Decryption requires only reversing the order in which the subkeys are applied.

Feistel Operation

1. 32 bits expanded to 48 bits using a padding scheme which repeats some bits
2. XOR the 48 bits with the 48-bit subkey
3. Break 48 bits into 8 blocks of 6 bits
4. Each block $W_i$ transformed using substitution table $S_i$, resulting in blocks of length $4$ and hence a total of 32 bits.
   • A transformation table is used to determine the output value
   • If the input block is $W = x_1x_2x_3x_4x_5x_6$, the row number is given by $x_1x_6$ and the column number by $x_2x_3x_4x_5$
5. A permutation is applied to the result

Brute Force Attacks

Testing all the possible $2^k$ keys (where $k$ is the size of the key $K$). $k = 56$ is fairly small, requiring only $2^{k}/2 = 2^{55}$ trials on average - this was criticized from the start.

The key can be identified by using a small number of ciphertext blocks and looking for low entropy in the decrypted plaintext.

Double Encryption

Let $K_1$ and $K_2$ be two block cipher keys.

Encryption: $C = E(E(P, K_1), K_2)$.

If both keys have length $k$, exhaustive attacks require $2^{2k - 1}$ trials on average.

Meet-in-the-Middle Attack

Let $(P, C)$ is a single plaintext-ciphertext pair:

1. For each key $K$, store $C' = E(P, K)$ in memory
2. For any key $K'$, check if $D(C, K') = C'$ (i.e. matches any ciphertext stored in memory)
   • If this is found, $K$ is $K_1$ and $K'$ is $K_2$
   • Check if key values work for other $(P, C)$ pairs

Requirements:

• Storing one plaintext block for every key: $2^{56}$ 64-bit blocks
• An encryption operation for every key
• A decryption operation for every key

Expensive but still much cheaper than brute-forcing $2^{111}$ keys.

Triple Encryption

Requires three keys: $C = E(D(E(P, K_1), K_2), K_3)$. (symmetric so decryption/encryption doesn’t matter? TODO)

This increases the computational requirements enough to make it secure against MITM attacks.

NIST SP 800-131A (2015) approves two-key triple DES, where $K_1 = K_3$, only for legacy use. three-key triple DES is approved.

OpenSSL removed triple DES in 2016. Office 365 stopped using triple DES in 2018.

AES

Designed in an open competition after controversy over DES. Winning submission is ‘Rijndael’.

• 128-bit data block
• 128-, 192- or 256-bit master key
• Byte-based design
• Substitution-permutation network
  • Initial round key addition
  • 10, 12, or 14 rounds (depending on key size)
  • Final round

Algorithm

State Matrix

16-byte data block size arranged in a $4 \times 4$ matrix.

Mixture of finite field operations in $GF(2^8)$ and bit string operations.

Round Transformation

Each round has four basic operations:

1. ByteSub (non-linear substitution): substitute each byte wth a different value using a substitution table
2. ShiftRow (permutation): rotate first row right by zero bytes, second row right by one byte… (bytes wrap to left)
3. MixColumn (diffusion): each column is replaced with result of it being multiplied by a matrix
4. AddRoundKey: XORs array with round key

Substitution-permutation network with block length of $n = 128$ and sub-block length of $l - 8$.

S-box uses look-up table.

Key Schedule

Master key is 128/192/256 bits.

Each of the 10/12/14 rounds uses a 128-bit subkey. There is one subkey per round plus one initial subkey, all derived from the master key.

Security

Some weaknesses but no significant break; most serious real attacks can reduce effective key size by around two bits.

Vulnerable to related-key attack: attacker obtains a ciphertext encrypted with a key related to an actual key in a specified way.

Comparisons with DES

• Data block size: 64 vs 128 bits
• Key size: 56 vs 128/192/256 bits
• Design:
  • Both iterated ciphers
  • DES uses Feistel; AES uses SPN
  • AES substantially faster in both hardware and software