09. Hash Functions and MACs

Hash Functions

A public function $H$ such that:

• $H$ is simple and fast to compute
• $H$ takes as input message $m$ of arbitrary length and outputs a message digest $H(m)$ of fixed length

Security Properties

• Collision resistant: it should be infeasible to find any two values $x_1$ and $x_2$ such that $H(x_1) = H(X_2)$
• Second-preimage resistant: given a value $x_1$, it should be infeasible to find a different value $x_2$ such that $H(x_1) = H(x_2)$
• Preimage resistant (one-way): given a value $y$, it should be infeasible to find any input $x$ such that $H(x) = y$

If an attacker can break second-preimage resistance, they can also break collision resistance.

Birthday Paradox

If there is a group of 23 people, there is over a 50% chance that at least two people have the same birthday.

If choosing $\sqrt{|S|}$ values from a set $S$, the probability of getting two values the same is about half ($n \approx \sqrt{2|S| \cdot p_\text{collision}}$).

Hence, if $H$ is a hash function with an output size of $k$ bits, $2^{k/2}$ trials will be enough to find a collision half the time (assuming $H$ is a random function).

Today, $2^{128}$ trials is considered infeasible so hash functions should have an output of at least 256 bits for collision resistance.

In comparison, to get a 50% change of guessing the key of a block cipher requires only $2^{k - 1}$ trials, so hash functions require about double the number of bits compared to block ciphers for the same security.

Iterated Hash Functions

Iterated hash functions splits the input into fixed-size blocks and operates on them sequentially.

Merkle-Damgård Construction

A compression function $h$ taking fixed-sized inputs and applies them to the blocks of the message.

The compression function takes two $n$-bit input strings $x_1$ and $x_2$ and produces an $n$-bit output string $y$:

m = m_1 || m_2 || m_3 || … || m_l

       m_1    m_2    m_3       m_l pad+len
        |      |      |         |     |
        |      |      |         |     |
        v      v      v         v     v
IV ---> h ---> h ---> h --...-> h---> h ---> H(m)

Security: if the compression function $h$ is collision-resistant, then so is $H$.

Weaknesses:

• Length extension attacks: if padding appended but not message length, there is no difference in the output of the message and the message with the right padding added. Hence, if the message is $m \| p$, they can extend this to $m \| p \| z \| p'$, where $z$ is the additional contents added by the attacker. Since the hash is the full internal state of the hash function, the attacker can use the hash and continue calulating the rest of the hash for $z \| p'$, allowing them to create valid hashes without knowledge of $\text{IV}$ or the rest of the message. Adding message length stops this attack
• Second-preimage attacks: not as hard as they should be
• Collisions for multiple messages: not that too much more difficult than finding collisions for two messages

The Merkle-Damgård construction is used in MD5, SHA-1 and SHA-2.

Standardized Hash Functions

MDx Family

Proposed by Ron Rivest, widely used in the 1990s.

128-bit output, all broken.

Secure Hash Algorithm (SHA)

Based on MDx family, more complex design with 160 bit output.

SHA-0 introduced 1993, SHA-1 in 1995 with minor changes. Both broken.

SHA-2 Family

Standardized 2015.

Hash sizes of 224, 256, 384 or 512 bits.

Minimum recommended is SHA-256 (256 bit hash, 512 bit blocks) - same security as AES-128.

Most secure is SHA-512: 512 bit hash, 1024 bit blocks.

Padding:

• Message length field: 64 bits for 512 bit blocks, 128 bits for 1024 bit blocks.
• Always at least one bit of padding
• There is one 1 bit, some number of 0 bits (enough to make blocks full) and then the length field
• Padding and length fields may add an extra block

SHA-3

MDx, SHA families based on the same basic design which were vulnerable to a few unexpected attacks.

Keccak function picked by NIST in 2015 as as SHA-3: uses sponge function instead of compression.

Using Hash Functions

Hash functions do not depend a key; anyone can calculate it so it is not encryption.

However, it does help to provide data authentication:

• Authenticating the hash of a message to authenticate the message
• Building blocks for MACs
• Building blocks for signatures

Password storage:

• Pick random salt: makes it resistant to rainbow table attacks as there needs to be a different dictionary for every salt
• Compute $h = H(\text{password}, \text{salt})$
• Store salt and hash value

Message Authentication Code

Ensures message integrity. takes in a message $M$ of arbitrary length and secret key $K$ and outputs a fixed-sized tag $T = \mathrm{MAC}(M, K)$.

The tag $T$ is appended to the message and the recipient can compute $T'$ with the message they receive and their shared secret, checking to ensure that $T' = T$.

Unforgeability: not feasible to produce a valid pair $(M, T)$ such that $T = \mathrm{MAC}(M, K)$ without knowledge of $K$.

Unforgeability under chosen message attack: even with access to an oracle that can calculate the MAC for an input message of the attacker’s choosing, they cannot create a valid tag themselves (i.e. guess the private key from tags they ask the oracle to generate).

MAC from Hash Function (HMAC)

Proposed by Bellare, Canetti and Krawczyk in 1996.

Can be built from any iterated hash function $H$.

With a key $K$ that has been padded with zeroes to be the required block size and two fixed strings:

• opad = 0x5c5c...5c
• ipad = 0x3636...36

HMAC is secure if $H$ is collision resistant or $H$ is a pseudorandom function. It is designed to resist length-extension attacks, even if $H$ is a Merkle-Damgård construct.

HMAC is often used as a pseudorandom function to derive subkeys.

Authenticated Encryption

A and B share a key $K$ and $A$ wishes to send a message $M$ with confidentiality and authenticity/integrity.

Two options:

• Split $K$ into $K_1$ and $K_2$, encrypting $M$ with $K_1$ and using $K_2$ with a MAC
• Use an authenticated encryption algorithm that provides both

Combining Encryption and MAC

Three options:

• Encrypt-and-MAC: encrypt $M$, apply MAC to $M$ and send the ciphertext $C$ and tag $T$
  • Encryption algorithms usually have an IV but MACs usually don’t; if the same message is sent multiple times the MAC will be the same
• MAC-then-encrypt: calculate the MAC on $M$, encrypt $M \| T$ then send the ciphertext $C$
• Encrypt-then-MAC: encrypt $M$, calculate the MAC on the ciphertext $C$ and then send $C$ and tag $T$

Encrypt-then-MAC is the safest option: $C = E(M, K_1)$, $T = \mathrm{MAC}(C, K_2)$, send $C \| T$

MAC-then-encrypt was used in older versions of TLS while newer versions use authentication encryption modes.

https://crypto.stackexchange.com/questions/202/should-we-mac-then-encrypt-or-encrypt-then-mac

CTR Mode for Block Ciphers

Synchronous stream cipher. Counter initialized with random nonce $N$, keystream generated by encrypting successive values of the counter:

where $t$ is the block number.

Encryption and decryption is simply XORing the plain/ciphertext with $O_t$.

Galois Counter Mode (GCM)

CCM mode cannot be used for processing of streaming data: formatting function for $N$, $A$ and $P$ requires knowledge of the length of $A$ and $P$.

Combines CTR mode on the block cipher $E$ with a special keyed hash function GHASH (uses multiplication in finite field $\mathrm{GF}(2^{128})$.

• Input: plaintext $P$, authenticated data $A$, nonce $N$
• Outputs: ciphertext $C$, tag $T$
• Lengths $\mathrm{len}_A$ and $\mathrm{len}_C$ are 64 bit values
  • $u$ and $v$ are the minimum numbers of zeros required to expand $A$ and $C$ to complete blocks
• Length $t$ of $T$ is 128 bits, $N$ is 96 bits long
• Initial block input: $J_0 = N \| 0^{31} \| 1$
• Function $\mathrm{inc}_{32}$ increments 32 MSB of the input string by $1 \pmod{2^{32}}$

GHASH:

$HK = E(0^{128}, K)$ is the hash subkey. $\cdot$ is multiplication in the finite field.

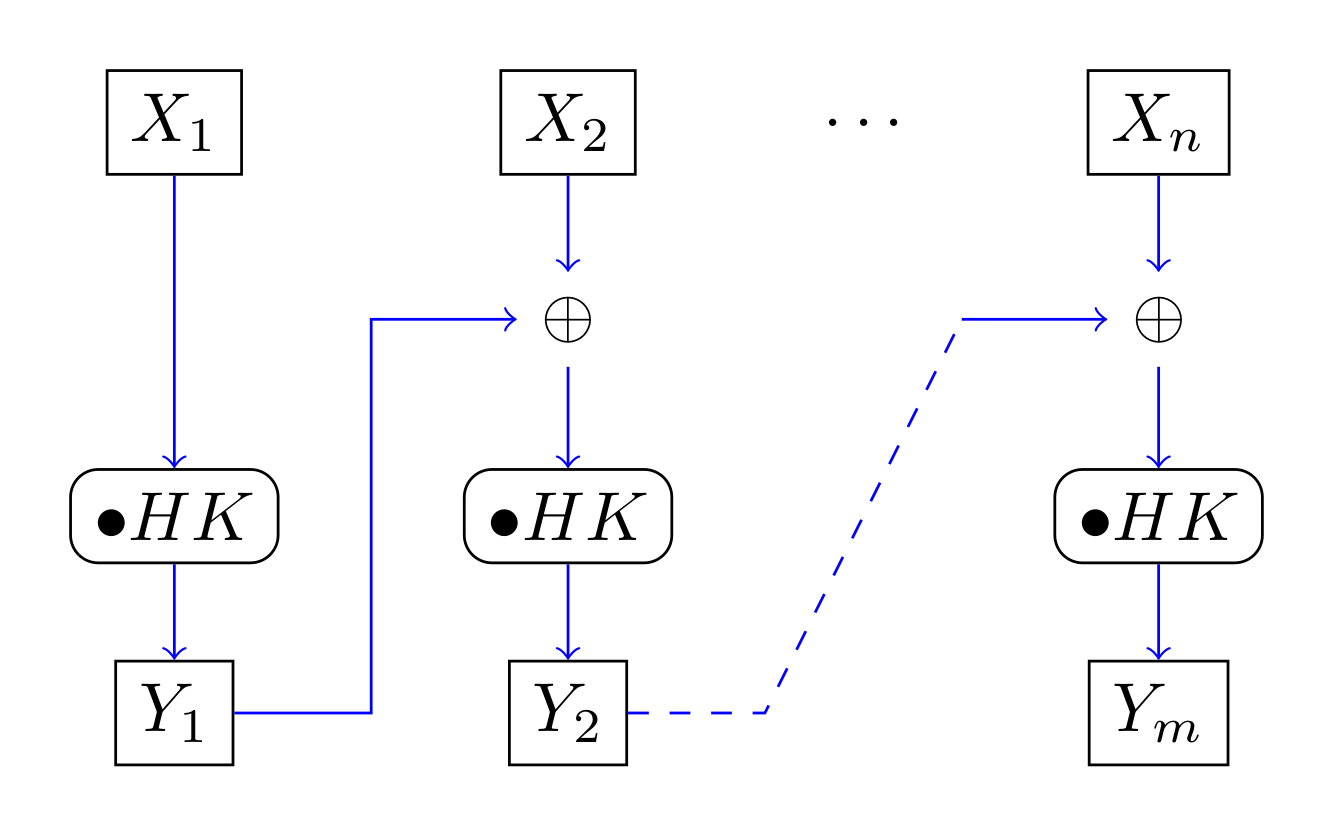
Output is $Y_m = \mathrm{GHASH}_{HK}(X_1, \dots, X_m)$

Decryption:

• Receiver receives ciphertext $C$, nonce $N$, tag $A$, authenticated data $A$
• Receiver computes tag $T'$ using shared key $K$, compares with $T$
• If the same, $P$ can be computed by generated the same keystream from CTR mode