01. Introduction
Lecturer: Clementine Gritti.
Course weighting:
- Quizzes: 20%
- 9 quizzes, 10 multi-choice questions with 4 options and 1 correct answer
- Assignment: 20%
- Released a week before the term break, due the week after
- Lab attendance: 10%
- If lab is missed, report can be emailed to course coordinator and TA by the following Friday
- Final Exam: 50%
CIA Triad:
- Loss of Confidentiality: when unauthorized people can access the data
- Loss of Integrity: when unauthorized changes can be made to the data
- Loss of Availability: when authorized users cannot access the data
02. Course Overview
What is Cyber security?
The NIST (National Institute of Standards and Technology) computer security handbook defines it as protections afforded to an information system to preserve confidentiality, integrity, availability (CIA) of system resources.
Terminology:
- Threat: potential security harm to an asset/system resource
- Attack: thread that is carried out. If successful, leads to undesirable violation of security
- Countermeasure: means taken to deal with attacks (prevention, detection, recovery)
- Vulnerabilities:
- Leaky: access to information given when it should not
- Corrupted: does the wrong thing or gives wrong answers
- Unavailable: impossible/impractical to access
Key questions:
- What assets need to be protected
- How are the assets threatened
- How can the threats be countered
Assets include:
- Hardware
- Software: OS, system utilities, applications
- Data: files, DB
- Networks: local/wide area network links, bridges, routers etc.
Types of Attacks
Passive:
- Does not alter information or resources in the system
- Hard to detect, easy to prevent
- Types of passive attacks:
- Eavesdropping/interception: attacker directly accesses sensitive data in transit
- Traffic analysis/inference: observations of the amount of traffic between the source and destination
Active:
- Alters information or system resources
- Hard to prevent, easy to detect
- Types of active attacks:
- Masquerade: attacker claims to be a different entity
- Message modification (falsification): message modified in transit
- DDoS (misappropriation): attacker prevents legitimate users from accessing resources
Inside:
- Initiated by entity inside the security perimeter
- Authorized to use the systems, but used in a malicious way
- Types of inside attacks:
- Exposure: sensitive data intentionally released to outsider
- Falsification: data altered or replaced
Outside:
- Initiated from outside the perimeter by an unauthorized or illegitimate user
- Types of outside attacks:
- Obstruction: communication links disabled, or communication control information altered
- Intrusion: attacker gains unauthorized access to sensitive data
Fundamental Requirements
Information security management requires:
- Threat identification
- Classification by likelihood and severity
- Security controls applied based on cost-benefit analysis
Countermeasures to threats and vulnerabilities:
- Computer security technical measures (access control, authentication etc.)
- Management measures (awareness, training)
What is Information Security?
ISO security architecture defines:
- Security: when vulnerabilities in assets/resources are minimized
- Asset: anything of value
- Vulnerability: any weakness that could be exploited to violate a system or its information
- Threat: potential security violation
Hence, information security is security where the assets/resources are information systems
Security Services and Mechanisms
OSI Security Architecture X.800: dated, but most definitions/terminology still relevant. Defines security threats, services, and mechanisms.
Security Services
A security service is processing/communication service that gives a specific kind of protection to system resources.
Security services include:
- Peer entity authentication: confirms entity is who they claim to be
- Data origin authentication: confirms origin of data unit/message
- Access control: protects against unauthorized use of resources
- Data confidentiality: protects data against unauthorized disclosure
- Traffic flow confidentiality: protects disclosure of data that can be derived from knowledge of traffic flow
- Data integrity: detects modification/reply of data in messages
- Non-repudiation: protects against the message creator falsely denying to creating the data
- Availability: protects against DDoS
- Encipherment: transforms data to hide its content
- Digital signature: mechanism to transform data using a signing key
From Stack Exchange:
- Non-repudiation: entity cannot deny to having sent/signed the message
- Message (or data origin) authentication: entity originally made the message
- Entity authentication: entity involved in current communication session
Security Mechanisms
A security mechanism is a method of implementing one or more security services.
Security mechanisms include:
- Data integrity: corruption-detection techniques
- Message Authentication Codes
- Authentication exchange: protocols to ensure identify of participants
- TLS
- Traffic padding: spurious traffic generated to protect against traffic analysis; usually used in combination with encipherment
- Control lists, passwords, tokens which indicate access rights
- Routing control: use of specific secure routes
- Notarization: use of trusted third party to assure source/receipt of data
03. Number Theory and Finite Fields
Discrete mathematics: cyroptology deals with finite objects (e.g. alphabets, blocks of characters)
Modular arithmetic; deals with finite number of values.
Basic Number Theory
Factorization
Given
An integer
Properties
If
If
Division algorithm
Given
Greatest Common Divisor
-
and - If
and , then -
Euclidean Algorithm
To find
Hence,
In psuedo-code:
def gcd(a, b):
r[-1] = a
r[0] = b
k = 0
while r[k] != 0:
q[k] = floor(r[k - 1]/r[k])
r[r + 1] = r[k - 1] - q[k]r[k]
k = k + 1
k = k - 1
return r[k]
Back-Substitution
Find
Can be rewritten as:
Example:
Back-substitution:
The result shows that
Modular Arithmetic
Given
In other words,
Residue Class
The set
The set
Groups
A group
- Closure:
for any and all - Identity: there is an element
such that for any and all - Inverse: there is an element
such that for any and all - Associativity:
for any and all
A group is abelian when it is the operation is commutative;
Cyclic Groups
The order
The order
A group is cyclic if it has a generator.
Computing Inverses Modulo
The inverse if
Theorem: let
The Euclidean algorithm can be used to find the inverse of
If
Hence, starting from
Group of Primes Modulus
Properties:
-
-
is cyclic -
has many generators (in general)
It can be thought of as the multiplicative group of integers
Finding Generators
A generator of
Lagrange theorem: the order of any element must exactly divide
To find a generator of
- Compute all distinct prime factors
of -
is a generator iff for all
Example
Find a generator for
-
: not a generator as -
: and so is a generator
Groups of Composite Modulus
For any non-prime
Properties:
-
is a group -
is not cyclic in general - Finding its order is difficult
e.g.
Example
Find a generator for
-
: not a generator as -
: -
-
-
-
-
-
- Hence, the order of
is equal to , cycling through all elements in the group before repeating - NB: every element is guaranteed to be in
as it is a group and hence has closure over the multiplication operation
-
Fields
A field
-
is an abelian group under the operation with the identity element -
is an abelian group under the operation with identity element - Distributivity:
for
Theorem: only finite fields of size
Finite Field
For a finite field
- Multiplication and addition are done modulo
- Its multiplicative group is exactly
Finite Field
- Addition modulo
: XOR ( ) - Multiplicative group:
Finite Field
Arithmetic in this field is considered as polynomial arithmetic where the field elements are polynomials with binary coefficients. e.g.
Properties:
- Polynomial division can be done easily using shift registers
- Adding two strings: add their coefficients modulo
(XOR) - Multiplication with respect to a generator polynomial
- AES uses
- AES uses
- Multiplying two strings: multiply them as polynomials, then take remainder of division by
03. Classical Encryption
Terminology
- Cryptography: the study of designing systems
- Cryptoanalysis: the study of breaking systems
- Steganography; the study of concealing information; not covered in this course
Cryptography transforms data based on a secret called the key. It provides confidentiality and authentication:
- Confidentiality: key needed to read the message
- Authentication: key needed to write the message
Cryptosystems:
- A set of plaintexts holding the original message
- A set of ciphertexts holding the encrypted message
- Sometimes called cryptogram
- A set of keys
- A function called the encryption or encipherment which transforms the plaintext into a ciphertext
- An inverse function called the decryption or decipherment which transforms the ciphertext into the plaintext
Symmetric key cipher (secret key cipher):
- Encryption/decryption keys known only to the sender/receiver
- Secure channel required for transmission of keys
Asymmetric key cipher (public key cipher):
- Each participant has a public and private key
- Can be used to both encrypt messages and create digital signatures
Notation for Symmetric Encryption Algorithms
- Encryption function
- Decryption function
- Message/plaintext
- Cryptogram/ciphertext
- Shared secret key
Encryption:
Decryption:
Methods of Cryptanalysis
What resources are available to the adversary? Computational capabilities, inputs/outputs to the systems, etc.
What is the adversary aiming to achieve? Retrieving the whole secret key? Distinguishing between two messages?
Exhaustive Key Search
Adversary tries all possible keys. Impossible to prevent such attacks; can only ensure there are enough keys to make exhaustive search too difficult computationally.
Note that the adversary may find the key without exhaustive search or even break the cryptosystem without finding the key.
Preventing exhaustive key search is a minimum standard.
Attack Classification
Ciphertext only attack: the attacker has access only to intercepted ciphertexts.
A cryptosystem is highly insecure if it can be practically attacked using only intercepted ciphertexts.
Known plaintext attack: the attacker knows a small amount of plaintexts and their corresponding ciphertexts.
Chosen plaintext attack: the attacker can obtain the ciphertext from some plaintext it has selected (attacker has ‘inside encryptor’).
Chosen ciphertext attack: the attacker can obtain the plaintext from some ciphertext it has selected (attacker has ‘inside decryptor’).
A cryptosystem should be secure against chosen plaintext and ciphertext attacks.
Kerckhoff’s Principle
Kerckoff’s Principle states the that the attacker has complete knowledge of the cipher; the decryption key is the only item unknown to the attacker.
Secret, non-standard algorithms are often flawed, providing mainly security through obscurity.
Alphabets
Historical ciphers: define alphabet for the plaintext and ciphertext
Roman alphabet:
- Sometimes it includes spaces, upper/lowercase characters, punctuation
- Sometimes maps the alphabet to numbers:
Statistical attacks depend on using the redundancy of the alphabet:
- Distribution of single letters, digrams, trigrams are used
- Exact statistics vary by sample
Basic Cipher Operations
Transposition: characters in plaintext are mixed up with each other (permutations)
Substitution: each character is replaced by a different character
Transposition Cipher
Permuting characters in a fixed period
The plaintext is seen as a matrix with
Key is
There are
Cryptanalysis
Frequency distribution of ciphertext and plaintext characters are the same.
If
Knowledge of plaintext language digram/trigrams can help to optimize trials.
Simple Substitution Ciphers
Each character in plaintext alphabet replaced by character in ciphertext alphabet using a substitution table.
This is called a monoaphabetic substitution cipher.
Caesar cipher:
-
th letter of the alphabet mapped to the th letter using the key - Encryption:
- Decryption:
- Guess
by finding the most frequent character in the ciphertext and mapping it to the most frequent character in the language (e.g. (space), ‘e’)
Random simple substitution cipher:
- Each character assigned to a random character of the alphabet
- Encryption/decryption done using substitution table
- If the alphabet has
characters, there are keys - One-to-one mapping, so second character can only be assigned to
characters
- One-to-one mapping, so second character can only be assigned to
- Caesar cipher is a special case of the random simple substitution cipher
- Frequency analysis: use the most frequent characters, common di/trigrams such as ‘the’
Polyalphabetic Substitution
Multiple mappings from plaintext to ciphertext: smoothens frequency distribution.
Typically periodic substitution ciphers based on a period
Given
A plaintext message:
it is encrypted to:
If
Key generation:
- Select block length
- Generate
random simple substitution ciphers
Encryption: encrypt the
Decryption: use the same substitution table as encryption.
Vigenère Cipher
Based on shifted alphabets.
The key
Let
e.g. if
Cryptanalysis
Identifying period length:
- Kasiski method
- Cryptool uses autocorrelation to automatically estimate period
Once period identified, the
Autocorrelation
Given ciphertext
English is non-random; there is better correlation between two texts with the same shift size.
Find peaks in the value of
Kasiski Method
If you identify sequences of characters that occur multiple times, find the distance between them; the period is likely to be a multiple of the period.
If you find multiple sequences with different distances, the period is likely to be a common divisor.
Once the period is found, the separate alphabets can be attacked separately; at this point, it is just a Caesar cipher.
Other Ciphers (for use by hand)
Beaufort cipher: like Vigenère, but
Autokey: starts off as the Vigenère cipher, but the plaintext defines the subsequent alphabet. Hence, the cipher is not periodic.
Running key cipher: practically infinite set of alphabets generated from a shared key. This is ofen an extract from a book called the book cipher.
Rotor Machines
Enigma: each character encrypted with a different alphabet with a period of ~17,000; would never repeat in the same message (in practice).
Hill Cipher
Polygram/polygraphic cipher: simple substitution of an extended alphabet consisting of multiple characters.
Has linearity, making known plaintext attacks easy.
Given
Encryption: multiplying the
Decryption: multiplying the matrix
Example
Each plaintext pair written as column vector. If there are insufficient letters, they are filled with uncommon letters (e.g.
Plaintext:
Encryption:
Decryption:
Cryptanalysis
Known plaintext attacks possible given
-
-
-
, so
Then
Comments:
- The plaintext message
may not be invertible - Ciphertext-only attacks follow known plaintext attacks with the extra task of finding probable blocks of matching plaintext-ciphertext
- e.g. if
, the frequency distribution of non-overlapping pairs of ciphertext characters can be compared with the distribution of pairs of plaintext characters
- e.g. if
- Cryptool defaults to an alphabet of
(where is space)
05. Block Ciphers
Main bulk encryption algorithms used in commercial applications. AES is one example of such algorithm.
Principles
Block ciphers are symmetric key ciphers where each block of plaintext encrypted with the same key.
A block is a set of plaintext symbols of a fixed size, typically 64 to 256 bits in modern ciphers.
They are used in configurations called modes of operation.
Notation
-
: plaintext block of length bits -
: ciphertext block of length bits -
: key of length bits - Encryption:
- Decryption:
Criteria
Shannon defined two encryption techniques:
- Confusion: substitution used to make the relationship between
and as complex as possible. - Diffusion: transformations used to dissipate the statistical properties of
across .
Repeated use of techniques can be used using the concept of a product cipher.
Product & Iterated Ciphers
Product Cipher
Cryptosystem where encryption performed by applying/composing several sub-encryption algorithms: output of one block used as input to next block.
Often composed of simple functions
Iterated Cipher
Special product ciphers called iterated ciphers where:
- Encryption divided into
similar rounds - Sub-encryption functions are the same function
: the round function - Each round key/subkey
is derived from the master key using a process called key schedule
Encryption
Given plaintext block
Decryption
There must be an inverse function
Types of Iterated Ciphers
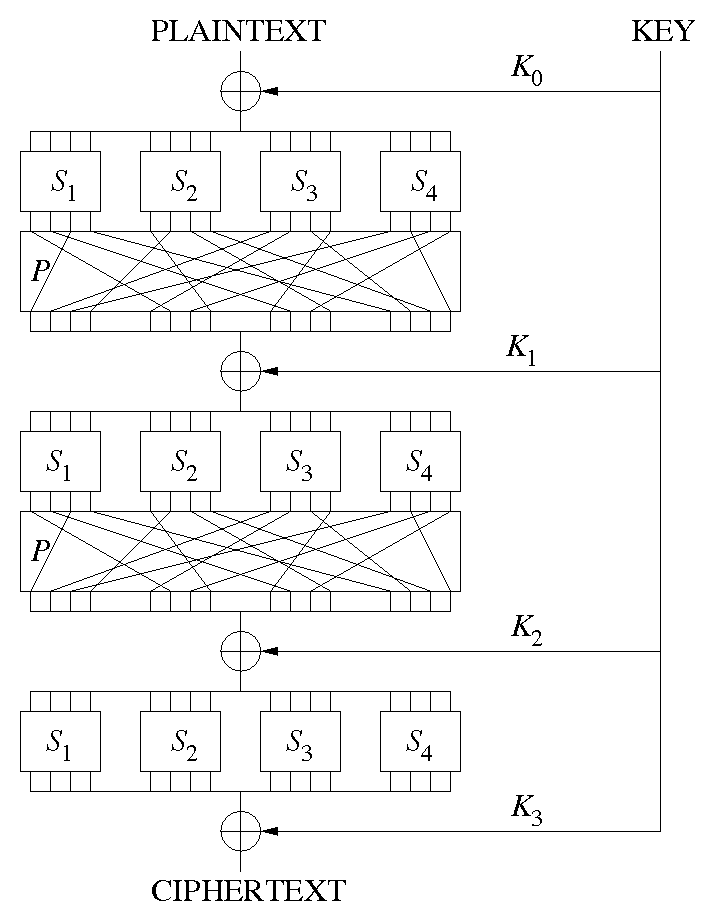
Substitution-Permutation Network (SPN) e.g. Advanced Encryption Standard (AES).
Feistel Cipher e.g. Data Encryption Standard (DES).
Substitution-Permutation Network
Block length
Substitution
i.e. mapping some binary number of size
Permutation
i.e. swapping the order of bits in the entire block around.
Operation
- Round key
XORed with current state block : - Each sub-block substituted applying
- The whole block permuted using
Example
- 4 round keys
- 4 S-boxes
- 1 P-box
- Last round does have a P-block
Feistel Cipher
Round function swaps the two halves of the block to form a new right hand half.
Encryption
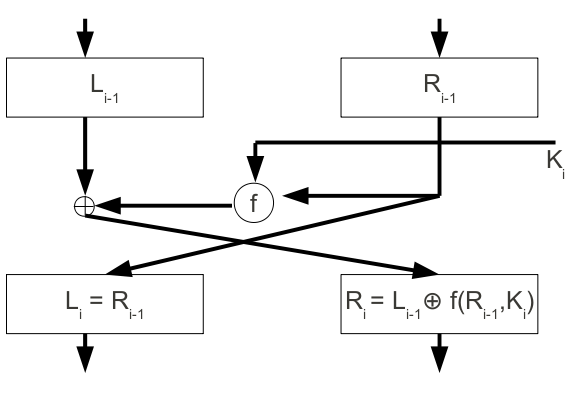
Plaintext block
For each round:
The output is the ciphertext block
Decryption
Split
For each round:
The choice of
Differential and Linear Cryptanalysis
Differential cryptanalysis: chosen plaintext attack using correlation in the differences between two input plaintexts and their corresponding ciphertexts.
Liner cryptanalysis: known plaintext attack that theoretically break DES.
Modern block ciphers normally immune to both attacks.
Avalanche Effects
Key avalanche: a small change in key (with the same plaintext) should result in a large change in ciphertext.
Plaintext avalanche: a small change in plaintext should result in a large change in ciphertext: changing one bit should change all bits in the ciphertext with a probability of
Key avalanche is related to Shannon’s notion of confusion, plaintext avalanche to Shannon’s notion of diffusion.
DES
Designed by IBM researchers, became US standard in 1976. 16-round Feistel cipher with key length of 56 bits and data block length of 64 bits.
The key length is actually 64 bits, but the last bit of every byte is redundant.
Encryption
- All bits of
permuted using an initial fixed permutation of - 16 rounds of Feistel operations applied, denoted by function
- Each round uses a different 48-bit subkey
- The subkey is defined by a series of permutations and shifts
- A final fixed inverse permutation
is applied
The 64-bit ciphertext block
Decryption requires only reversing the order in which the subkeys are applied.
Feistel Operation
- 32 bits expanded to 48 bits using a padding scheme which repeats some bits
- XOR the 48 bits with the 48-bit subkey
- Break 48 bits into 8 blocks of 6 bits
- Each block
transformed using substitution table , resulting in blocks of length and hence a total of 32 bits. - A transformation table is used to determine the output value
- If the input block is
, the row number is given by and the column number by
- A permutation is applied to the result
Brute Force Attacks
Testing all the possible
The key can be identified by using a small number of ciphertext blocks and looking for low entropy in the decrypted plaintext.
Double Encryption
Let
Encryption:
If both keys have length
Meet-in-the-Middle Attack
Let
- For each key
, store in memory - For any key
, check if (i.e. matches any ciphertext stored in memory) - If this is found,
is and is - Check if key values work for other
pairs
- If this is found,
Requirements:
- Storing one plaintext block for every key:
64-bit blocks - An encryption operation for every key
- A decryption operation for every key
Expensive but still much cheaper than brute-forcing
Triple Encryption
Requires three keys:
This increases the computational requirements enough to make it secure against MITM attacks.
NIST SP 800-131A (2015) approves two-key triple DES, where
OpenSSL removed triple DES in 2016. Office 365 stopped using triple DES in 2018.
AES
Designed in an open competition after controversy over DES. Winning submission is ‘Rijndael’.
- 128-bit data block
- 128-, 192- or 256-bit master key
- Byte-based design
- Substitution-permutation network
- Initial round key addition
- 10, 12, or 14 rounds (depending on key size)
- Final round
Algorithm
State Matrix
16-byte data block size arranged in a
Mixture of finite field operations in
Round Transformation
Each round has four basic operations:
- ByteSub (non-linear substitution): substitute each byte wth a different value using a substitution table
- ShiftRow (permutation): rotate first row right by zero bytes, second row right by one byte… (bytes wrap to left)
- MixColumn (diffusion): each column is replaced with result of it being multiplied by a matrix
- AddRoundKey: XORs array with round key
Substitution-permutation network with block length of
S-box uses look-up table.
Key Schedule
Master key is 128/192/256 bits.
Each of the 10/12/14 rounds uses a 128-bit subkey. There is one subkey per round plus one initial subkey, all derived from the master key.
Security
Some weaknesses but no significant break; most serious real attacks can reduce effective key size by around two bits.
Vulnerable to related-key attack: attacker obtains a ciphertext encrypted with a key related to an actual key in a specified way.
Comparisons with DES
- Data block size: 64 vs 128 bits
- Key size: 56 vs 128/192/256 bits
- Design:
- Both iterated ciphers
- DES uses Feistel; AES uses SPN
- AES substantially faster in both hardware and software
06. Block Cipher Modes of Operation
Block ciphers encrypt single blocks of data, but many applications require multiple blocks to be encrypted sequentially and breaking the plaintext into blocks and encrypting them separately can be insecure.
Modes of operation are standardized with different security and efficiency characteristics.
NIST has many standards (e.g. SP 800-38 series) for this.
Important Features of Different Modes
Different modes can provide confidentiality, authentication (and integrity) or both.
Modes for confidentiality normally include randomization.
Different modes have different efficiency and communication properties.
Randomized Encryption
Problem: the same plaintext block is encrypted to the same ciphertext block every time - allows patterns to be found in long ciphertexts.
Prevention: randomizing encryption schemes by using an initialization vector (IV) which propagates through the entire ciphertext. It may need to be either random or unique.
Alternatively, there could be a variable state which is updated with each block.
Efficiency
Parallel processing: encrypting/decrypting multiple plaintext/ciphertext blocks in parallel.
Error propagation: a bit error in the ciphertext which results in multiple bit errors in the plaintext after decryption.
Padding
Requiring the plaintext to consist of complete blocks.
NIST suggested padding method: append a single
Notation
- Plaintext message
of length blocks -
-th plaintext block for - Ciphertext message
-
-th ciphertext block for - Key
- Initialization vector
Modes can be applied to any block cipher.
Confidentiality Modes
Electronic Code Book (ECB) Mode
A basic mode of a block cipher; each block is encrypted with a key, IV is not used.
Encryption
Decryption
Properties
| Randomized | Padding | IV | Parallel encryption | Parallel decryption |
|---|---|---|---|---|
| No | Required | None | Yes | Yes |
Error propagation: within blocks.
Cipher Block Chaining (CBC) Mode
Blocks chained together: the plaintext XORed with previous ciphertext (or IV for the first block) and then encrypted.
Encryption
for
Decryption
Where
Properties
| Randomized | Padding | IV | Parallel encryption | Parallel decryption |
|---|---|---|---|---|
| Yes | Required | Random | No | Yes |
Error propagation: within blocks and into specific bits in the next block.
Parallel decryption means that decryption does not require the plaintext of previous block. However, it does require the ciphertext of the previous block.
Commonly used for bulk encryption, was often used in TLS up to TLS 1.2.
Counter (CTR) Mode
Synchronous stream cipher mode.
Encryption
The counter and a nonce (IV) are initialized using a random value
That is,
Then, this result is encrypted with the key
Finally, it is XORed with the plaintext block
Decryption
Properties
| Randomized | Padding | IV | Parallel encryption | Parallel decryption |
|---|---|---|---|---|
| Yes | Optional | Unique | Yes | Yes |
A one-bit change in ciphertext produces one-bit change in the plaintext at the same location.
This allows access to specific plaintext blocks without decrypting the whole stream.
CTR mode is the basis for authenticated encryption in TLS 1.2.
Authentication Mode
Message Integrity
Ensuring messages are not altered in transmission: preventing an adversary from re-ordering, replacing, replication and deleting message blocks to alter the received message.
Message integrity and authentication are treated as the same thing.
Proving message integrity is independent from using encryption for confidentiality.
Message Authentication Code (MAC)
Where
The output
Given both parties share the key
- The sender computes
- The message
and tag are sent - The receiver computes
on the received message and checks that
MAC Properties
Only the sender and receiver can produce
If
It has the basic security property of unforgeability: it is infeasible to produce
Basic CBC-MAC
Using block cipher to create a MAC providing message integrity (but not confidentiality).
If
For
It is unforgeable as long as the message length is fixed.
- If the IV is random, the IV needs to be sent along with the MAC
-
- Hence, the attacker can modify
and together such that XORing them gives the same result. As is not modified, none of the subsequent ciphertexts (and hence the tag) stays unchanged
Cipher-based MAC (CMAC)
Standardized, NIST version of CBC-MAC. The IV is all zeroes. The below is as per RFC4493.
Two keys
For
For the final block:
(That is, 1 and then enough zeros to fill up a block)
Then do the same operation as with the previous blocks , except that
Finally,
NIST allows the length of the tag,
The standard recommends the MAC tag
-
is a limit on how many invalid messages are detected before is changed -
is the acceptable probability that a false message is accepted
Authenticated Encrypted Mode
Two types of input data:
- Payload: both encrypted and authenticated
- Associated data: only authenticated
NIST specifies two modes:
- NIST SP-800-38C (2004) for Counter with CBC-MAC
- NIST SP-800-38D (2007) for Galois/Counter (GCM)
Both use CTR mode but add integrity in different ways.
Both are used in TLS 1.2 and 1.3.
Counter with CBC-MAC (CCM) Mode
CBC-MAC for authentication of all data, CTR mode encryption for the payload.
Inputs:
- Nonce
for CTR mode - Payload
of bits - Associated data
Compute the CBC-MAC tag, getting
Split the message
Then, use CTR mode to compute blocks.
From RFC3610:
- Authentication using CBC-MAC:
-
Blocks
generated. contains the metadata such as the nonce, payload length etc. Later blocks contain the payload and associated data.
-
- Encryption using CTR mode:
- Generate a keystream
where is the block number. - Output message
. starts with , not - Output authentication value
- Generate a keystream
- Decryption requires key
, nonce , authenticated data and ciphertext - Authenticated data must be sent separately!
CCM Mode Format
Lengths of
If
e.g. TLS 1.2:
07. Pseudorandom Numbers and Stream Ciphers
Random Numbers
Randomness: want any specific string of bits is exactly as random as any other string.
True random number generator (TRNG): physical process which outputs each valid string independently with equal probability.
Pseudorandom number generator (PRNG): deterministic algorithm which approximates a TRNG.
For practically, TRNGs are often used to provide a seed for a PRNG.
Pseudorandom Number Generator (PRNG)/Deterministic Random Bit Generator (DRBG)
Entropy source includes:
- Physical noise source
- Digitization process
- Post-processing stages
Periodic health tests required to ensure reliable operation.
Each generator takes a seed as an input, outputting a bit string before updating its state.
The seed should be updated after some number of calls.
DRBGs expose some functions:
- Instantiate: set the initial state using a seed
- Generate: provide bit string for each request
- Reseed: input new random seed and update the state
- Test: check correct operation
- Uninstantiate: delete/zeroising the state
The DDRBG should prevent an attacker from being able to reliably distinguish between its output and a truly random string. There are two types of resistance:
- Backtracking resistance: attacker with access to current state of DRBG should not be able to distinguish between the output of earlier calls and random strings
- Forward prediction resistance: attacker with access to current state of DRBG should not be able to distinguish between output of later calls and random strings
CTR_DRBG
Block cipher in counter (CTR) mode - AES with 128-bit keys recommended.
DRBG initialized with seed whose length is equal to key length PLUS block length.
Seed defines a key
CTR run iteratively with no plaintext.
Update Function
Each request to the DRBG generates up to
State
Up to
Dual_EC_DRBG
Older standard based on elliptic curve discrete logarithm problem and with many flaws.
Much slower than other DRBGs.
Secret deal between NSA and RSA Security to use this as the default PRNG in their software was reported in 2013.
Stream Ciphers
Generates keystream using a short key and initialization vector
Each element of the keystream is used to successively encrypt one or more ciphertext characters.
Stream ciphers are usually symmetric.
Synchronous Stream Ciphers
Keystream is generated independently of the plaintext; both the sender and receiver need to generate the same keystream and be synchronized.
Keystream and plaintext are XORed together, so receiver simply needs to XOR the ciphertext with the keystream to decrypt.
Vigenère cipher can be seen as a periodic synchronous stream cipher where each shift is defined by a key letter.
CTR mode of operation for a block cipher can be used to generate a keystream.
Binary Synchronous Stream Ciphers
For each time interval
-
is the binary keystream -
is the binary plaintext -
is the binary ciphertext
Encryption:
Decryption:
One-Time Pad
Key is random sequence of characters such that each is independently generated.
Each character in the key is only used once; this provides perfect secrecy.
Alphabet can be of any length but is usually either binary or a natural language alphabet.
Perfect Secrecy
Shannon’s definition:
-
Message set
-
Ciphertext set
-
; probability that is encrypted given that is observed - In most cases, messages
are not equally likely; that is, given a ciphertext, some messages are more likely than others
- In most cases, messages
-
For all messages
and ciphertexts :
The ciphertext should be independent of the plaintext
One-Time Pad Perfect Secrecy
Let a ciphertext
The probability that
As each keystream is chosen with equal probability,
Any keystream is possible and so given any plaintext, every possible ciphertext is generated with equal probability.
Vernam Binary One-Time Pad
- Plaintext : binary sequence
- Ciphertext: binary sequence
- Keystream : binary sequence
- Must be same length as the plaintext
- Encryption:
- Decryption:
Properties
Shannon showed that any ciphertext with perfect secrecy must have as many keys as there are messages. Hence, one-time pad is the only unbreakable cipher.
However, this requires secure communication between fixed parties and secure key generation, transportation, synchronization, and destruction which are all difficult due to the size of the keys.
Visual Cryptography
Encryption splits an image into two shares, each pixel being shared in a random way (similar to splitting a bit in a one-time pad).
Each share alone reveals no information about the image, but the two images can be overlayed to reveal the plaintext.
Prominent Stream Ciphers
A5 Cipher
Binary synchronous stream cipher applied in most GSM communications. Three variants:
- A5/1 is the original algorithm defined in 1987
- A5/2 is the weakened version intended for deployment outside Europe
- A5/3 (KASUMI) used in 3G systems
A5/1 Design
Three linear feedback shift registers (LFSRs) whose outputs are combined.
The LFSRs are irregularly clocked, making the overall output non-linear.
It has a 64-bit keystream such that 10 bits are fixed to zero; hence, the effective key length is 54 bits.
RC4 Cipher
Ron’s code #4 . Originally owned by RSA but leaked in 1994. Too weak to use in real systems nowadays, but was was widely deployed in TLS before 2013.
ChaCha Algorithm
Possible replacement of RC4 designed in 2008.
Faster than AES; as few as 4 cycles/byte on x84 processors.
Number Theory for Public Key Cryptography
- Number theory problems used in public key cryptography
- Need efficient ways of generating large prime numbers
- Definitions of hard computational problems are the base of crypto systems
Chinese Remainder Theorem (CRT)
Let
Let
Given integers
Where:
Condensed Equation:
Example
Find
-
and -
and are relatively prime so CRT can be used -
For
Make sure you replace
For
Example 2
Find
Hence
Where:
-
- As
,
- As
-
- As
,
- As
Hence:
Test:
-
as required -
as required
Euler Function
Given the positive integer
e.g.
Properties
if
e.g. for
Fermat’s Theorem
Let
Euler’s Theorem
More general case of Fermat’s theorem.
If
Primality Tests
Testing for primality by trial division not practical for large numbers.
There are many probabilistic methods, although these may fail in exceptional circumstances.
Agrawal, Saxena, Kayal 2002: polynomial time deterministic primality test, although still impractical.
Fermat Primality Test
Fermat’s little theorem: if
If
The probability of failure can be reduced by repeating the test with different base values of
Given the number
- Pick
at random such that - If
, return as being composite. Otherwise, return probable prime - The powers can be reduced using the following properties:
-
- The powers can be reduced using the following properties:
Some composite numbers such as
Example
Check if
Using
Hence it is composite, so we do not need to make further checks.
Miller-Rabin Test
Most widely used test for generating large prime numbers. It is guaranteed to detect composite numbers of the test is run sufficiently many times.
Modular square root of
There are four square roots of
- Two are
and - Two are called non-trivial square roots of
If
Miller-Rabin Algorithm
Let
- Pick
at random such that - Set
- If
, return probable prime - For
to : - If
, return probable prime - Else, set
- If
- Return composite
If the test returns probable prime,
If
As the algorithm is run
In practice, the error probability is smaller: when
Why The Miller-Rabin Test Works
Given a random
Hence,
Each number on the sequence is the square of the previous number (modulo
If
- Either
OR - There is a square root of
somewhere in the sequence whose value is (which is equal to
If a non-trivial square root of
Example
Let
- Choose
-
-
so: -
-
-
-
- Hence,
will never occur - Hence,
must be composite
-
NB:
Example 2
Let
Let
-
- This is not
so: - Repeat up to
times: -
Hence,
Generation of Large Primes
- Choose a random odd integer
of the same number of bits as the required prime - Test if
is divisible by any of a small list of primes - If not:
- Apply the Miller-Rabin test five random or fixed based values of
- If
fails any test, set and return to step 2
- Apply the Miller-Rabin test five random or fixed based values of
This incremental method does not produce completely random primes. If this is an issue start from step 1 if
Basic Complexity Theory
Two aspects:
- Algorithmic complexity: how long does it to take to run a particular algorithm
- Problem complexity: how long does it to take to run the best known algorithm for the given problem
Express this complexity using ‘big O’ notation; in terms of the space and time required to solve the problem for a given size.
Hard Problems
Integer factorization: given an integer of
Discrete logarithm problem (base 2): given a prime
There are no known polynomial algorithms to solve the problems; the best known algorithms are sub-exponential.
Factorization Problem
Trial by division: exponential time algorithm
Some fast methods exist, although they only apply to integers with particular properties.
Bets known general method: number field sieve, a sub-exponential algorithm.
As
Discrete Logarithm Problem
Given a prime
Given
, find such that .
(i.e. find the power given the remainder)
This can be written as
If
Example
Find
Hence
Example 2
Find the discrete logarithm of the number
i.e. solve
There is a cycle with powers of
09. Hash Functions and MACs
Hash Functions
A public function
-
is simple and fast to compute -
takes as input message of arbitrary length and outputs a message digest of fixed length
Security Properties
- Collision resistant: it should be infeasible to find any two values
and such that - Second-preimage resistant: given a value
, it should be infeasible to find a different value such that - Preimage resistant (one-way): given a value
, it should be infeasible to find any input such that
If an attacker can break second-preimage resistance, they can also break collision resistance.
Birthday Paradox
If there is a group of 23 people, there is over a 50% chance that at least two people have the same birthday.
If choosing
Hence, if
Today,
In comparison, to get a 50% change of guessing the key of a block cipher requires only
Iterated Hash Functions
Iterated hash functions splits the input into fixed-size blocks and operates on them sequentially.
Merkle-Damgård Construction
A compression function
The compression function takes two
m = m_1 || m_2 || m_3 || … || m_l
m_1 m_2 m_3 m_l pad+len
| | | | |
| | | | |
v v v v v
IV ---> h ---> h ---> h --...-> h---> h ---> H(m)
Security: if the compression function
Weaknesses:
- Length extension attacks: if padding appended but not message length, there is no difference in the output of the message and the message with the right padding added. Hence, if the message is
, they can extend this to , where is the additional contents added by the attacker. Since the hash is the full internal state of the hash function, the attacker can use the hash and continue calulating the rest of the hash for , allowing them to create valid hashes without knowledge of or the rest of the message. Adding message length stops this attack - Second-preimage attacks: not as hard as they should be
- Collisions for multiple messages: not that too much more difficult than finding collisions for two messages
The Merkle-Damgård construction is used in MD5, SHA-1 and SHA-2.
Standardized Hash Functions
MDx Family
Proposed by Ron Rivest, widely used in the 1990s.
128-bit output, all broken.
Secure Hash Algorithm (SHA)
Based on MDx family, more complex design with 160 bit output.
SHA-0 introduced 1993, SHA-1 in 1995 with minor changes. Both broken.
SHA-2 Family
Standardized 2015.
Hash sizes of 224, 256, 384 or 512 bits.
Minimum recommended is SHA-256 (256 bit hash, 512 bit blocks) - same security as AES-128.
Most secure is SHA-512: 512 bit hash, 1024 bit blocks.
Padding:
- Message length field: 64 bits for 512 bit blocks, 128 bits for 1024 bit blocks.
- Always at least one bit of padding
- There is one
1bit, some number of0bits (enough to make blocks full) and then the length field - Padding and length fields may add an extra block
SHA-3
MDx, SHA families based on the same basic design which were vulnerable to a few unexpected attacks.
Keccak function picked by NIST in 2015 as as SHA-3: uses sponge function instead of compression.
Using Hash Functions
Hash functions do not depend a key; anyone can calculate it so it is not encryption.
However, it does help to provide data authentication:
- Authenticating the hash of a message to authenticate the message
- Building blocks for MACs
- Building blocks for signatures
Password storage:
- Pick random salt: makes it resistant to rainbow table attacks as there needs to be a different dictionary for every salt
- Compute
- Store salt and hash value
Message Authentication Code
Ensures message integrity. takes in a message
The tag
Unforgeability: not feasible to produce a valid pair
Unforgeability under chosen message attack: even with access to an oracle that can calculate the MAC for an input message of the attacker’s choosing, they cannot create a valid tag themselves (i.e. guess the private key from tags they ask the oracle to generate).
MAC from Hash Function (HMAC)
Proposed by Bellare, Canetti and Krawczyk in 1996.
Can be built from any iterated hash function
With a key
opad = 0x5c5c...5cipad = 0x3636...36
HMAC is secure if
HMAC is often used as a pseudorandom function to derive subkeys.
Authenticated Encryption
A and B share a key
Two options:
- Split
into and , encrypting with and using with a MAC - Use an authenticated encryption algorithm that provides both
Combining Encryption and MAC
Three options:
- Encrypt-and-MAC: encrypt
, apply MAC to and send the ciphertext and tag - Encryption algorithms usually have an IV but MACs usually don’t; if the same message is sent multiple times the MAC will be the same
- MAC-then-encrypt: calculate the MAC on
, encrypt then send the ciphertext - Encrypt-then-MAC: encrypt
, calculate the MAC on the ciphertext and then send and tag
Encrypt-then-MAC is the safest option:
MAC-then-encrypt was used in older versions of TLS while newer versions use authentication encryption modes.
https://crypto.stackexchange.com/questions/202/should-we-mac-then-encrypt-or-encrypt-then-mac
CTR Mode for Block Ciphers
Synchronous stream cipher. Counter initialized with random nonce
where
Encryption and decryption is simply XORing the plain/ciphertext with
Galois Counter Mode (GCM)
CCM mode cannot be used for processing of streaming data: formatting function for
Combines CTR mode on the block cipher
- Input: plaintext
, authenticated data , nonce - Outputs: ciphertext
, tag - Lengths
and are 64 bit values -
and are the minimum numbers of zeros required to expand and to complete blocks
-
- Length
of is 128 bits, is 96 bits long - Initial block input:
- Function
increments 32 MSB of the input string by
GHASH:
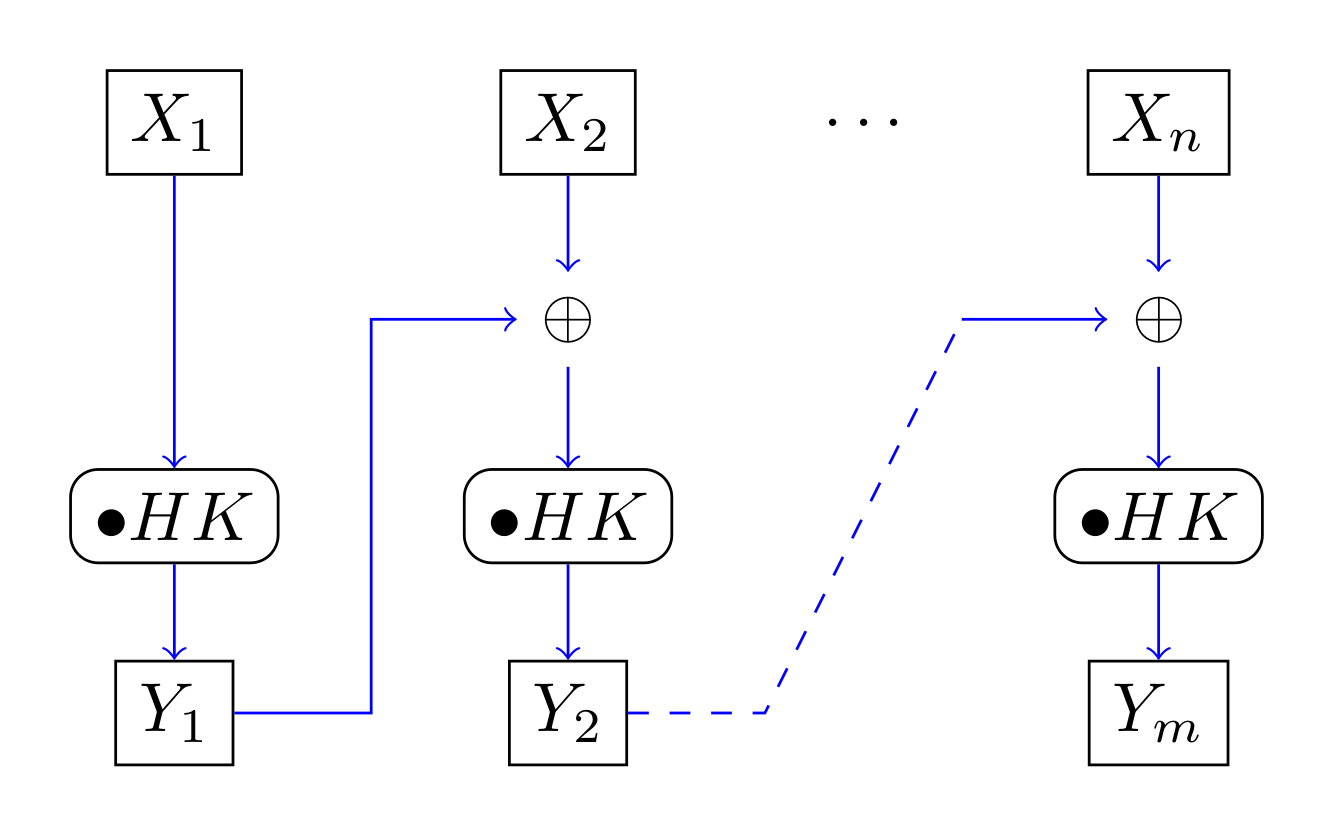
Output is
Decryption:
- Receiver receives ciphertext
, nonce , tag , authenticated data - Receiver computes tag
using shared key , compares with - If the same,
can be computed by generated the same keystream from CTR mode
10. Public Key Cryptography
Public key cryptography (PKC) has some features that symmetric key cryptography (SKC) does not and is applied for key management in protocols such as TLS and IPsec.
Discrete log-based ciphers are alternatives to PKC.
One-Way Functions
A function is one-way if
It is not known if one-way functions exist, but there are many functions that are believed to be one-way:
- Multiplication of large primes: the inverse function is integer factorization
- Exponentiation: the inverse function takes discrete logarithms
Trapdoor One-Way Functions
A function such that
Example: let
- The inverse function will be to find
such that - From Euler’s theorem,
for any integer , assuming co-prime to - Hence,
( and are co-prime to each other) -
for some integer - That is,
- Hence,
-
- Integer factorization is assumed to be a hard problem; hence
cannot be computed easily - Hence, only someone with knowledge of
’s factors, the trapdoor, can find the inverse function
Asymmetric Cryptography
Another word to describe public key cryptography.
Public key cryptosystems, such as the Diffie-Hellman key exchange, are designed by using a trapdoor one-way function: the trapdoor is the decryption key.
This allows a public key to be stored in a public directory: anyone can obtain the public key and use it to form an encrypted message that only a person with the private key can decrypt.
Asymmetry: encryption and decryption keys are different. Encryption key is public and known to anybody; the decryption key is private and known only to its owner.
Finding the private key from the public key must be a hard computational problem.
Advantages of shared key/symmetric cryptography:
- Key management is simplified: they dot not need to be transported confidentially
- Digital signatures can be obtained
RSA
Designed in 1977 by Rivest, Shamir, and Adleman from MIT (patent expired 2000).
It is based on integer factorization problem.
Algorithm
Key generation:
- Randomly choose two distinct primes,
and from the set of all primes of a certain size - Compute
- Randomly choose
such that - Compute
- Set the public key
- Set the private key
Encryption:
- Input is value
such that - Compute
Decryption:
- Compute
Any message must be pre-processed:
- Coding it as a number
- Adding randomness (to avoid repeating ciphertext for the same plaintext)
Numerical Example
Key generation:
- Let
, -
-
- Let
-
(Solve using the Euclidean algorithm)
-
Encryption:
- Let
-
Decryption:
Numerical Example 2
Key generation:
- Let
, -
-
- Let
-
Find
-
Solve
using the Euclidean algorithm:
-
Encryption:
- Let
-
Decryption:
Correctness
Decrypting an encrypted message: does
As
Hence,
Now we must show that
Case 1: Coprime to n
Case 2: Multiple of p or q
Since
Supposing that
Applying Fermat’s theorem,
As
- There is a unique solution
to: -
-
- Hence,
-
- And
is satisfied too
Applications
- Message encryption
- Digital signature
- Distribution of key for symmetric key encryption (hybrid encryption)
- User authentication
Implementation
A few implementation details
Key Generation
Generating large primes
- At least 1024 bits recommended for today
- Simple algorithm: select random odd number
of required length, check if prime, incrementing by two if not
Choice of
- Choose at random for best security
- But small values are often used in practice: more efficient
-
is smallest possible value; very fast but has security issues -
is a popular choice -
should be at least to prevent known attacks such as Wiener’s attack
Encryption/decryption
Fast Exponentiation
A square-and-multiply modular exponentiation algorithm.
In binary,
If
Code:
// 2^66 % 100
M = 2 // base
n = 100 // modulus
e = [0, 1, 0, 0, 0, 0, 1] // exponent as bits, LSB first
z = 1; // Result - M^e \bmod n
for(let i = 0; i < e.length - 1; i++) {
if(e[i] == 1) {
z = (z * M) % n;
// z = 1 initially so first multiplication is unnecessary
// Hence e.filter(i => i == 1).length - 1 multiplications
}
M = (M * M) % n; // equals base^{2^{i + 1}}
// When i = 0, M = base^1 - right for the next iteration
// Does not need to be calculated for the i + 1 == e.length
// as the value is used for the next iteration
}
Cost:
- If
the algorithm uses squarings - If
bits of are high, there are multiplications (first computation has , but is initially one) -
is 2048 bits so is at most 2048 bits. Hence, computing requires at most 2048 modular squarings or multiplications - On average, only half of
’s bits are high so there are only 1024 multiplications
Faster Decryption Using CRT
Decrypting
Compute
Solve
Hence,
Then we can output
Speedup
Exponents
Hence, computing each of
Hence, storing
Padding
Encryption directly on the message encoded as a number is bad as it is vulnerable to attacks:
- Building up a dictionary of known plaintexts
- Guessing the plaintext and checking if it encrypts to the ciphertext
- Håstad’s attack
Hence, a padding mechanism must be used to prepare the message for encryption, adding redundancy and randomness.
Håstad’s Attack
The same message
Equations can be solved using the CRT to obtain
Padding Types
- PKCS 1: simple ad-hoc design
- Optimal asymmetric encryption padding (OAEP):
- Bellaware and Rogaway, 1994
- Security proof in a suitable model
- Standardized in IEEE P1363
Security
Attacks
Mostly avoided through the use of standardized padding mechanisms.
Possible attacks:
- Factorization of the modulus
: this is believed to be a hard problem, so should be fine as long as is large enough. - Finding
from and : as hard as factorizing (Miller’s theorem) - Quantum computers: Shor’s theorem can theoretically factorize
in polynomial time - Timing analysis: using timing of decryption process to obtain information about
- Demonstrated in practice in smart cards
- Avoided by randomizing the decryption processes
Practical Problems with Key Generation
- OpenSSL implementation in some systems would use massively-reduced randomness (2008)
- Lenstra in 2012 analyzed 6 million RSA keys:
- Found 4% of keys were identical
- Found 0.2% of keys provided no security as they shared one prime factor with each other
Diffie-Hellman Key Exchange
Two users sharing a secret using only public communication.
Public elements:
- Large prime
- Generator
Alice and Bob randomly select values
Over an insecure channel, Alice sends
Both compute the secret key
Example
Let
- Alice sends
- Bob sends
Both compute
Properties
Security
Relies on the difficulty of the discrete logarithm problem.
If an attacker intercepts
There is no better known way for a passive adversary to find the shared secret.
Authenticated Diffie-Hellman
In the basic protocol, messages are not authenticated: a man-in-the-middle-attack is possible where the attacker acts as a proxy between the two parties, decrypting messages from one party and then re-encrypting messages to send to the other party with the other key.
- Alice chooses
, sending and - Bob chooses
, sending , and - Alice sends
- Both computes
Both parties must know each other’s public signature verification keys,
Static and Ephemeral Diffie-Hellman
The above protocol uses ephemeral keys: keys are used once. In the static protocol:
- Alice chooses a long-term private key
and public key - Bob chooses a long-term private key
and public key - Alice and Bob find a shared secret
which is static -
stays the same until either party changes their public key
-
Elgamal Cryptosystem
Proposed by Elgamal in 1985, turning the Diffie-Hellman protocol into a cryptosystem for encryption and for signature.
Alice combines her ephemeral private key with Bob’s long-term public key
Algorithms
Key generation:
- Select prime
, generator - Select long-term private key
- Compute
- Set the long-term public key
Encryption:
- Select a message
- Choose at random an ephemeral private key
- Compute
and - Compute the ciphertext:
-
Decryption:
- Compute
-
Correctness
- Alice knows ephemeral private key
- Bob knows long-term private key
- Both compute the Diffie-Hellman value for the two public keys:
-
- Diffie-Hellman value
used as the mask for the message
Example
Key generation:
- Prime
- Generator
- Long-term private key
- Compute
- Bob’s public key is
Encryption:
-
Alice wants to send
-
chosen at random -
Computes
Decryption:
-
Bob computes
-
Bob recovers
Security
- Dependent on the difficulty of the discrete logarithm problem: if broken, they could determine the private key
from - Many users could share the same
and - Padding not required: ephemeral key
randomizes the ciphertext
Elliptic Curves
Algebraic structures formed from cubic equations.
Curves are defined over any field.
e.g. set of all
A point on the curve is the identity element, and by defining a binary operation on the points (e.g. multiplication), we can form a group over elliptic curve’s points: the elliptic curve group.
Any elliptic curve can be used but most applications use standardized curves generated in a verifiably random way (e.g. NIST curve P-192 has curve of
Discrete log defined on elliptic curve groups: if elliptic curve operation operation denoted as multiplication, definition is the same as in
Elliptic curve implementations require smaller keys compared to RSA:
| Symmetric key | RSA modulus | EC element length |
|---|---|---|
| 80 | 1024 | 160 |
| 128 | 3072 | 256 |
| 192 | 7680 | 384 |
| 256 | 15360 | 512 |
From Ars:
- Symmetric across horizontal axis
- Any non-vertical line intersects with the curve at most three times. Group operation:
- Infinity,
, is the identity element - Draw line intersecting the two points
- If the points are the same, use the tangent
- Find the third point intersecting the line
- If the points are the same and it is at an inflection point, use the same point
- Find the opposite point
- Infinity,
11. Digital Signatures
MACs allow entities with shared secrets to generate valid tags, providing data integrity and authentication.
Digital signatures use public key cryptography to provide additional properties: only the owner of a private signing key can generate a valid signature.
Non-repudiation: the signer cannot deny they have signed a message.
Properties
Algorithms: Key & signature generation, signature verification.
Key generation algorithm outputs a private signing key,
Signature generation:
Signature verification:
Correctness: if
Unforgeability: computationally infeasible to generate signature for any message without key. Note that the signing algorithm may be randomized - many possible signatures for a message.
Stronger security definition: forging a new signature should be difficult even if they can obtain signatures for messages of their choice (chosen message oracle).
Security Goals
Key recovery: recovering the private signing key
Selective forgery: choosing a message and obtaining a signature for that message.
Existential forgery: forging a signature on any message not previously signed (even a meaningless message).
Modern digital signatures should be able to resist existential forgery under a chosen message attack.
RSA Signatures
Key Generation
Key generation is the same as for encryption keys:
- Public verification key:
, where is the product of two large primes and - Private signing key:
, , such that
A fixed public parameter, the hash function
Signature Generation and Verification
Given message
Given claimed signature
Discrete Logarithm Signatures
Three versions:
- Original Elgamal signatures in
(1985) - Digital signature algorithm (DSA) standardized by NIST
- DSA based on elliptic curve groups: ECDSA
Elgamal Elements in
-
is a large prime -
is a generator of -
is the private signing key, where -
is part of the public key - A message
in
Signature generation:
-
Pick random
such that -
Compute
-
Solve
for : -
Output the tuple
Signature verification: check if
Correctness
Fermat’s Little Theorem
Fermat’s little theorem: given a prime
if
Proving Correctness
Let
Hence, coming back to the Elgamal signature verification equation (and noting that
as required.
Digital Signature Algorithm (DSA)
Published by NIST in 1994. Based on Elgamal signatures but calculations are simpler and signatures shorter: done in a subgroup of
Prime
Generator
where
Let
Both sides of the equation are reduced modulo
Key generation:
- Choose secret key
- Compute the public key,
.
Signature generation:
- Message
- Pick
- Compute
- Why
?
- Why
- Compute
- Set the signature as
Signature verification:
- Check if
, - Compute
- Compute
- Compute
- Check that
Verification equation is the same as with Elgamal except that all exponents and the final result is reduced modulo
Correctness
Fermat’s Little Theorem
Where
Hence
Proving Correctness
Let
Hence, coming back to the Elgamal signature verification equation (and noting that
as required.
Elliptic Curve DSA (ECDSA)
Similar to DSA except that:
-
becomes the order of the elliptic curve group - Multiplication modulo
is replaced by the elliptic curve group operation - After operations on group elements, only the
coordinate is kept from the pair
Compared to DSA, public keys are shorter but signatures are not (326 to 1142 bits).
12. Public Key Infrastructure and Certificates
Public Key Infrastructure (PKI)
NIST: “… key management environment for public key information of a public key cryptographic system”
Must consider:
- Key lifecycle: generation, distribution, storage and destruction
- Trusted legal/business entities:
- Registration Authorities (RAs): vouch for the identify of a user
- Validation Authorities (VAs): verify identities
- Certification Authorities (CAs): issue digital certificates (certifying public key TODO?)
Digital Certificates
How do you confirm the relationship between the public key and the claimed owner of that key? Through the use of digital certificates:
- Contain public key and owner identity
- Metadata such as signature algorithm, validity period
Certificates are signed by a certification authority (that should be trusted by the certificate verifier).
Certification Authority
A CA creates, issues and revokes certificates for subscribers and other CAs.
A CA has a certification practice statement (CPS) which covers processes such as checks before issuing certificates, physical/procedural security controls, revocation processes.
X.509 Certificate
Now RFC 5280, currently on version 3.
Important fields:
- Version number
- Serial number
- Signature algorithm identifier
- Issuer name (CA name)
- Subject name (user to which the certificate is issued)
- Public key information
- Validity period
- Digital signature (generated by CA)
Verification:
- Check CA signature is valid
- Requires user to have public key of the CA
- Check any conditions set in the certificate (e.g. validity period) are correct
Certification paths: CAs can issue certificates to other CAs. Hence, as long as there is a chain of CAs leading to a trusted root CA, the last CA can be trusted and hence the certificate can be validated.
Phishing: attacker can make URL and interface similar to a genuine site
Extended validation certificates: certificate issued by only some CAs after they have validated the entity’s legal identity. Different icon in browsers, but mostly ignored by users.
Revocation:
- Certificate marked as invalid even if its validity period is current
- User must check which certificates have been revoked
- Certificate Revocation List (CRL): each CA issues list of revoked certificates that must be downloaded by clients
- Online Certificate Status Protocol (OCSP): server responds to requests about specific certificates
Public Key Pinning:
- Depreciated feature that allowed websites to tell browsers to fix the public key used to verify certificates
- If CA was compromised, attacker can issue another certificate for the website but the browser would continue to use the pinned key for some time period
PKI Examples
Hierarchical PKI:
R Root
/ \
/ Y Intermediate
A \ CAs
Z
/ \
B C Users
CA certifies public key of entity below. If non-hierarchical, certification can be done between any CAs.
Browser PKI:
- Multiple hierarchies with preloaded public keys as root CAs
- Intermediate CAs can be added
- Users can add their own certificates
- Most servers send their public key and certificate through TLS
OpenPGP PKI:
- Used in PGP emails
- Certificate includes ID, public key, validity period, self-signature
- NO certification authorities
- Various key servers store public keys
- Web of trust: users can attest to association between public key and username
13. Key Establishment
Distribution of cryptographic keys to protect subsequent sessions. In TLS, public keys allow clients/servers to share a new communication key.
Kerberos: key establishment without public keys.
Key Management
Key management has four phases:
- Key generation: keys should be generated such that they are all equally likely to occur
- Key distribution: keys should be distributed in a secure fashion
- Key protection: keys should be accessible only to authorized parties
- Key destruction: once a key has performed its function, it should be destroyed such that it (TODO the encrypted data?) has value to an attacker
Hierarchy
Keys often organized into a hierarchy. In a two-level hierarchy, there are long- and short-term keys:
- Long-term/static keys are used to protect the distribution of session keys. They may last anywhere from a few hours to a few years, depending on the application
- Short-term/session/ephemeral keys are used to protect communications in a session. They may last anywhere from a few seconds to a few hours, depending on the application
Key Establishment
Symmetric keys with ciphers (e.g. AES, MAC) are used in practice for session keys as as they are more efficient than public key algorithms.
Long-term keys can be symmetric or asymmetric.
Key Distribution Security Goals
Authentication: they should be able to authenticate that the receiver is the party they intended to send the key to.
Confidentiality: no adversary can obtain the session key accepted by a particular party.
In formal models, the protocol is broken if the adversary can distinguish the session key from a random string.
Mutual and Unilateral Authentication
Mutual authentication: both parties achieve the authentication goal.
Unilateral authentication: only one party achieves the authentication goal. This is done by most real-world key establishment protocols: typically clients authenticate the server with client authentication happening later.
Adversary Capabilities
A strong adversary knows the details of the cryptographic algorithms and can:
- Eavesdrop on all messages
- Alter messages sent
- Re-route messages to any other party
- Obtain the session key used in any previous run
Distribution of Pre-Shared Keys
A trusted authority (TA) generates and distributes long-term keys to all users when they join the system. Their involvement ends here in the pre-distribution phase so if there are no new users they can go offline.
A simple scheme is to assign a secret key for each pair of users, but this will not scale well as the number of keys grows quadratically.
Probabilistic schemes reduce key material at each party by forwarding messages to other parties that hopefully have a link to the final receiver. Hence, it offers only a high probability of a secure channel between any two parties and requires other nodes to be trusted as they must decrypt and re-encrypt the message. This is suitable for sensor networks.
Key Distribution using Symmetric Keys
Key distribution with online server.
A TA shares a long-term shared key with each user. They distribute session keys to users when requested and hence, the TA is highly trusted and is a single point of attack. Scalability may also be a problem.
Needham-Schroeder Protocol
Widely-known key establishment protocol published 1978. Found vulnerable to replay attacks in 1981 - attacker can replay old messages that a honest party will accept an old session key.
Notation:
- Two parties,
and - TA
-
and share a long-term key -
and share a long-term key - New session key
generated by - Nonce
, randomly generated by and respectively for one-time use -
: sends message to -
: message encrypted using key . There is assumed to be some authentication mechanism
Protocol:
Replay Attacks
If an attacker
To defend against this, the established key must be fresh for each session:
- Random challenges (nonces)
- Timestamps
- Counters
The repaired protocol uses random challenges. After
Tickets can also be used: if
Kerberos
Now on V5, released 1995. Standardized as RFC 4120. Used in Windows as the default domain authentication method.
Kerberos allows:
- Secure network authentication service in an insecure network
- Single sign-on: users only need to enter their username/password once per session
- Access to different online services using individual tickets
- Session keys to be established in an authenticated and confidential fashion
It is a 3-level protocol:
Level 1
Client
Where:
-
is the symmetric key shared between and , usually generated on login from -
is the symmetric key generated by -
is the nonce generated by to ensure is fresh -
is the long-term key shared between and -
is valid for some validity period .
At the end of this exchange,
Level 2
Client
Where:
-
is a session key shared between and -
is a long-term key shared between and -
is a nonce -
is a ticket for service with validity period -
where is a timestamp - The ticket-granting server must check that the timestamp is valid
The ticket-granting server must also check that the client has permission to access the service
In practice, the AS and TGS are the same machine.
Level 3
Client
Where:
The reply from
Limitations
Realms (domains over which an authentication server has authority to authenticate a user) must share keys with every other realm, so although multiple realms are supported it has limited scalability.
Key Distribution using Asymmetric Cryptography
No online TA is required. Instead, public keys (managed by PKI - certificates and CAs) is used for authentication. Users are trusted to generate good session keys (so hopefully each party has a good PRNG).
Key transport: user chooses key material and sends it to another party (encrypted, possibly signed). Does NOT provide forward secrecy.
Key agreement: Diffie-Hellman or some other protocol where both parties provide input to the key. The messages are signed, providing authentication. Provides forwards secrecy.
TLS supports both key transport and agreement.
Forward Secrecy
If a long-term key is compromised, the attacker can now claim to be the owner of the key. If key transport is used, all previous session keys will be compromised.
A protocol provides (perfect) forwards secrecy if compromise of the long-term secret keys do not reveal session keys previously agreed using the long-term keys.
Signed Diffie-Hellman
Computations done in
- Generator
- Random values
and chosen by each party where -
is a signature on message from signed with their signing/long-term key -
is a signature on message from signed with their signing/long-term key -
and are and ’s identities respectively - Both parties know each other’s public verification key
- Long-term signing keys provide only authentication, hence it has perfect forward secrecy
Protocol:
-
sends , -
sends , and -
checks signature. If valid, computes session key
-
- A sends
-
checks signature. If valid, computes session key
-
14. Transport Layer Security Protocol
The most widely used security protocol.
History:
- SSL 2.0 developed by Netscape in 1994, 3.0 in 1995
- Standardized as RFC 2246 in 1999, called TLS 1.0
- TLS 1.1 (4346) in 2006, fix issues with non-random IVs, weaknesses from padding
- (the below are good to use)
- TLS 1.2 (5246) in 2008 allows standard authenticated encryption
- TLS 1.3 (8446) in 2018 had major changes and separated key agreement and authentication algorithms
Overview
Three higher-level protocols:
- TLS handshake protocol
- TLS alert protocol signals events
- TLS change cipher spec protocol for changing cryptographic algorithm (not available in TLS 1.3)
TLS record protocol provides basic services to the higher-level protocols. Stack:
|----------------------------------------|
| TLS | TLS change | TLS | HTTP/ |
| Handshake | cipher | alert | Other |
|----------------------------------------|
| TLS record protocol |
|----------------------------------------|
| TCP |
|----------------------------------------|
| IP |
|----------------------------------------|
TLS Record Protocol
TLS offers:
- Message confidentiality - message contents cannot be read in transit
- Message integrity - receiver can detect modifications made to the message in transit
These services may be provided by a symmetric encryption algorithm (confidentiality) and MAC (authentication/integrity). TLS 1.2 and above offer authenticated encryption modes (CCM, GCM), combining these two services into one.
The handshake protocol establishes the symmetric session keys used by the record protocol.
The record protocol also deals with dividing messages into blocks and re-assembling received blocks and possibly with compressing/decompressing block contents.
Format
HEADER
|--------------------------------------|
| Content | Major | Minor | Length |
| type | version | version | |
|--------------------------------------|
ENCRYPTED CONTENTS
|--------------------------------------|
| Plaintext |
| (possibly compressed) |
| (not available in TLS 1.3) |
|--------------------------------------|
| MAC |
| (unless authentication encryption) |
|--------------------------------------|
Content type can be change-cipher-spec, alert, handshake or application-data.
TLS 1.3 does not allow the cipher suite to be changed to prevent downgrade attacks - a new session must be created.
Major version is 3 for TLS and minor version 1 to 4 for TLS 1.0 to 1.3.
Length of data is in octets.
Operation
- Each application-layer message is
bytes or less - Compression removed in TLS 1.3 after attacks discovered, null by default in TLS 1.2
- Authenticated data: data, header and implicit record sequence number
- Plaintext: data and MAC (unless using authenticated encryption)
- Session keys: established in handshake protocol
- One key for each of MAC and encryption for each direction
- A single key if using authenticated encryption
- Specification: encryption/MAC algorithms specified in negotiated cipher suite
MAC algorithm:
- SHA-2 allowed in TLS 1.2 and above
- MD5 and SHA-1 not supported in TLS 1.3
Encryption algorithm:
- Block cipher in CBC or a stream cipher
- Most common block cipher is AES
- 3DES and RC4 not supported in TLS 1.3
- For block ciphers, padding is applied after the MAC to get complete blocks
Authenticated encryption algorithm:
- Allowed instead of separate encryption and MAC algorithms in TLS 1.2 and above
- TLS 1.3 supports only AES with either CCM or GCM modes
- Authenticated data in header and implicit record sequence number
TLS Handshake Protocol
For:
- Negotiating the TLS version and cryptographic algorithms used
- Establishing a shared symmetric session key for use in the record protocol
- Authenticating the server and optionally authenticating the client
Many variations supported - many were dropped to in TLS 1.3.
Phases
- Phase 1: initiating the logical connection and establishing the capabilities of the partner
- Phases 2 and 3: performing the key exchange
- Operation depends on the handshake variant negotiated in phase 1
- Phase 4: completing setup
Cipher Suites
Specify the public key algorithms used for key establishment and symmetric algorithms used for authenticated encryption/key computation.
There were over 300 standardized cipher suites, many of which were discarded in TLS 1.3.
TLS 1.3 requires cipher suites to be Authenticated Encryption with Associated Data (AEAD). AEAD means that there is some associated data that must be sent in plain text (not confidential) but should be authenticated - for example, sequence numbers and other header information.
e.g. TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA384:
- Ephemeral elliptic curve Diffie-Hellman key transfer (new key for each session)
- Key exchange parameters signed using ECDSA (and server’s certificate is also signed by CA using ECDSA)
- AES with 256 bit key used as block cipher
- Cipher block chaining mode of operation
- SHA-2 with digest size of 384 used for the HMAC and for key generation/validation
- Hence required even if AEAD algorithm like GCM or CCM used
e.g. TLS_RSA_WITH_3DES_EDE_CBC_SHA:
- Mandatory in TLS 1.0/1.1
- RSA used for key exchange
- 3DES in CBC mode for encryption (confidentiality)
- SHA-1 used for HMAC (data integrity) and key generation/validation
Handshake algorithms:
- DHE-DSS: Diffie-Hellman key Exchange with Digital Signature Standard/Algorithm (TLS 1.2 only)
- DHE-RSA: Ephemeral Diffie-Hellman with RSA signatures (TLS 1.2/1.3)
- ECDHE-RSA: Elliptic Curve DHE with RSA signatures (TLS 1.2/1.3)
- ECDHE-ECDSA: Elliptic Curve DHE with Elliptic Curve Digital Signature Algorithm (TLS 1.2/1.3)
DH-RSA: permanent DH parameters part of the server certificate (signed with RSA), so there is no forwards secrecy.
Record algorithms:
- AES-CBC-SHA256: AES in CBC mode, SHA256 HMAC (TLS 1.2)
- AES-GCM: AES in GCM mode for authenticated encryption (TLS 1.2/1.3)
- CHACHA20-POLY1305: ChaCha stream cipher with Poly1305 MAC (TLS 1.2/1.3)
Forwards Secrecy:
- Compromise of a long-term key should not lead to compromise of session keys established prior to the compromise
- Diffie-Hellman handshakes offer forwards secrecy, but RSA-based handshakes do not. Hence, TLS 1.3 drops support for static RSA
Handshake
- Phase 1: client/server negotiate TLS version, cipher suite and compression, and exchange nonces
- Phase 2: server sends certificate and key exchange message (if required by cipher suite)
- Phase 3: client sends certificate and key exchange message (if required by cipher suite)
- Phase 4: secure communications. Finished messages also includes check value of all previous messages
Client hello (phase 1):
- Highest TLS version supported
- Cipher suites supported
- Client nonce
Server hello (phase 1):
- Selected TLS version and cipher suite
- Server nonce
Server key exchange (phase 2):
- Server inputs to key exchange
Client key exchange (phase 3):
- Client inputs to key exchange
Change cipher suite (phase 4):
- Use negotiated cipher suite for record layer
Ephemeral Diffie-Hellman Handshake Variant
Server key exchange; server sends:
- Diffie-Hellman generator
- Group parameters (e.g.
) - Server’s ephemeral Diffie-Hellman value
The response is signed by the server using their private key. The client must check this.
Client key exchange; client sends their ephemeral Diffie-Hellman value. Signed if the client has their own certificate.
Pre-master secret (
Steps:
- Client hello: TLS version, supported cipher suites, client nonce
- Server hello: server certificate, chosen cipher suite, server nonce
- Server signature:
, and server’s DH parameter signed using server private key - Client checks server signature, sends client’s DH parameter
- Pre-master secret calculated using DH parameters
- Session keys computed with PRF
- Client finished message: encrypted with session key
- Server finished message: encrypted with session key
RSA Handshake Variant
- Client hello: TLS version, supported cipher suites, client nonce
- Server hello: server certificate, chosen cipher suite, server nonce
- Client checks server certificate
- Pre-master secret key transport: client randomly chooses pre-master secret
, encrypted with server’s public key - Session keys computed with PRF
- Client finished message: encrypted with session key
- Server finished message: encrypted with session key
Other Handshake Variants
Diffie-Hellman: static/fixed Diffie-Hellman with certified keys. If the client does not have a certificate, they use an ephemeral Diffie-Hellman key.
Anonymous Diffie-Hellman: ephemeral Diffie-Hellman, but keys are not signed at all - only protects against passive eavesdropping.
Session Key Generation
Master secret
The
To generate the key material (the amount depends on cipher suite):
Independent session keys are partitioned from
Depending on cipher suite, key material may include encryption key, MAC key and IV.
The
e.g. for TLS 1.2:
TLS Alert Protocol
Alert messages of varying degrees of severity:
- Warning alerts
close_notifyalerts- Fatal alerts
If alert messages are handled improperly, users may be vulnerable to truncation attacks.
Attacks
Backwards Compatibility
Insecure versions of TLS are depreciated slowly:
- SSL 3.0 was depreciated in 2015
- End-of-life for TLS 1.0 and 1.1 was in 2020
TLS 1.2 is secure as long as a good cipher suite is used:
- RC4 shown to be vulnerable, offered in TLS 1.2
TLS 1.2 supported by 99.5% of websites, TLS 1.3 (released 2018) ~50% as of August 2021. See SSL Pulse for up-to-date statistics.
BEAST (Browser Exploit Against SSL/TLS)
Exploits non-standardized IV use in CBC mode encryption: IVs are chained from previous ciphertexts; attack could recover plaintext byte-by-byte.
Theoretical attack found in 2002 but required the full block to be guessed. In 2011 researchers found a method where they could have all but one byte in the block to be known, requiring only that byte to be guessed.
TLS 1.1 requires random IVs, and most browsers added mitigation strategies by putting only one byte of data in the first block (and padding the rest with random data) and the remaining bytes into the second block, forcing a randomized IV.
CRIME (Compression Ratio Info-leak Made Easy) and BREACH (Browser Reconnaissance and Exfiltration via Adaptive Compression of Hypertext)
Side channel attacks based on compression: different inputs result in different amounts of compression.
CRIME is based on compression in the TLS level, BREACH on compression at the HTTP level.
CRIME: attacker has ability to control part of request. If request gets smaller, the attacker-controlled content is probably matches part of source content (e.g. cookies).
TLS 1.3 does not allow compression. Disabling compression at a HTTP level results in a large performance hit.
POODLE (Padding Oracle On Downgraded Legacy Encryption)
A padding oracle enables an attacker to know if a message in a ciphertext was correctly padded.
Encryption in CBC mode can provide a padding oracle due to its error propagation properties: servers (after decrypt all blocks and validating the padding) may sometimes return an ‘invalid padding’ error.
Main mitigation is to have a uniform error response so that attacker cannot distinguish between padding and MAC errors.
Theoretical in 2002, practical in 2014 with POODLE, which forced a downgrade into SSL 3.0.
Heartbleed
Implementation error in OpenSSL found in 2014: improper input validation due to missing bounds check in heartbeat messages allowed memory leakage.
Heartbeats allow clients/servers to send a few bytes of data that the partner should echo back: OpenSSL did not validate that the length field matched actual length of the heartbeat, so the allocated memory could include freed data that contained sensitive data (e.g usernames/passwords, private keys).
Other Attacks
- Man-In-The-Middle (MITM)
- Found in 2015, Lenovo was bundling Superfish spyware in their computers, which including a self-signed root certificate that used the same private key across devices
- STARTTLS command injection
- Sweet32
- Triple Handshake
- RC4 attacks
- Lucky Thirteen
- Renegotiation
TLS 1.3
Drafted 2014, adopted as RFC 8446 in August 2018.
TLS 1.3 did a large spring cleaning, removing:
- Static RSA, Diffie-Hellman key exchange
- Cipher-suite renegotiation (
change-cipher-spec) - SSL negotiation
- DSA
- Data compression
- Non-AEAD (authenticated encryption with associated data) cipher suites
- AEAD is more efficient, secure, require less keys and are easier to implement compared to separate encryption and MACs algorithms.
- MD5, SHA-335 hash functions
- Change Cipher Spec protocol
TLS 1.3 also added:
- Separation of key agreement and authentication algorithms from cipher suites
- Mandating perfect secrecy: ephemeral keys during EC Diffie-Hellman key agreement
- Encrypting content type
- 0-RTT mode (using pre-shared key)
- Post-handshake client authentication
- ChaCha20 stream cipher with Poly1305 MAC
- Client hello:
- TLS version, supported cipher suites
- Key share:
- Guesses selected cipher suite (s), sends key share (s)
- If guess was wrong, server sends retry hello request
- Server hello:
- Selected TLS version, cipher suite
- Key share
- Everything after this in the handshake can be encrypted
- Server certificate (and optionally the certificates up the chain)
- Hash of handshake messages signed with server certificate
- Client handshake finished
- Hash of handshake messages signed with session key
0-RTT Overview
Even faster handshakes using pre-shared key (resumption master secret) obtained for the purpose of 0-RTT after a previous (and recent) connection.
TLS 1.3 1-RTT (with ephemeral Diffie-Hellman key exchange):
- Client hello
- Server hello plus:
- Diffie-Hellman key share
- Encrypted extensions
- Certificate
- Key to verify certificate
- Client response:
- Diffie-Hellman key share
- Certificate
- Verification data
TLS 1.2 1-RTT session resumption:
- Client hello plus:
- Diffie-Hellman key share
- Pre-shared key (from previous connection after handshake)
- Server hello
- Diffie-Hellman key share
- Encrypted extensions
TLS 1.3 0-RTT:
- Client hello:
- Key share
- Application data encrypted with resumption key negotiated previously
- End of early data alert
- Server hello:
- Key share
- Application data encrypted with session key
- Client handshake finished:
- And more application data
- Further messages encrypted with new session key
Limitations:
- Attackers can capture encrypted 0-RTT and re-send them to the server: if the server is misconfigured, it may accept the replayed requests
15. IPsec and VPN
IP security: framework for ensuring secure communications over IP networks; similar security services as TLS, but running at a lower level of the protocol stack.
VPNs: extending a private network across a public network.
IP Layer Security
TLS runs at the transport layer; IPsec runs at the network layer. Hence, it allows protection for any higher levels, including TCP and UDP.
Provides encryption, authentication and key management algorithms.
Standardized in 2005 with RFC 4301-4305; commonly used to provide VPNs.
Security services:
- Confidentiality: encryption to protect against unauthorized data disclosure
- Integrity: MACs to determine if data has been modified in transit
- Limited traffic analysis protection: difficult to know which parties are communicating, how often, or how much
- Possible by concealing IP datagram details (e.g. source/destination addresses)
- Message reply protection: data not delivered multiple times or badly out-of-order
- Peer authentication: each endpoint confirms its identity with the other IPsec endpoint
Architectures
Gateway-to-Gateway Architecture:
- Secure communication between two networks
- Protects only data between the two gateways
Host-to-Gateway Architecture:
- For secure remote access (e.g. VPN gateway) - allowing access to resources on secured networks from insecure networks
- Each remote access user establishes a connection to the gateway
Host-to-Host Architecture:
- Most secure but also most costly; typically used for special purpose needs e.g. remote management of a single server
- Provides end-to-end protection for data
- All user systems and servers need to have VPN software installed/configured; resource intensive to implement
- Key management through a manual process
Protocols
Encapsulating security payload (ESP): provides confidentiality, authentication, integrity and reply protection.
Authentication header (AH) (depreciated): authentication, integrity and reply protection, but NOT confidentiality.
Internet key exchange (IKE): negotiation, creation and management of session keys in security associations (SAs).
IPsec Connection Setup
With the IKEv2 protocol (RFC 7296, 2014):
- Diffie-Hellman protocol authenticated with X.509 certificates
- Includes cookies to mitigate DDOS attacks
- Provides proof of reachability before expensive cryptographic operations are run
- When server under load, server responds to initial respond with stateless cookie; cookie whose value can be derived from the initial request without storing responder-side state
- Client must repeat the request, but this time with the stateless cookie
- Proof of work: pre-image for a partial hash value (find message whose hash is less than a given value)
- Reduces the number of negotiations an attacker can initiate
Security Associations (SA)
Runs after connection setup allows keys to be established.
SAs contain information needed to support an IPsec connection.
It may include:
- Cryptographic keys and algorithms
- Key lifetimes
- Security parameter index (SPI)
- Security protocol identifier (ESP/AH)
SAs tells the endpoint how it should process inbound IPsec packets and/or generate outbound packets.
SAs are unidirectional: there is one SA for each direction.
Cryptographic Suites
Cryptographic suites in IPsec are:
- Similar to TLS cipher suites
- Allow specific groups for Diffie-Hellman (both finite field and symmetric key)
- 3DES and AES for encryption in CBC or GCM mode
- HMAC or CMAC used for integrity if GCM mode not used
Modes of Operation
ESH and AH can run in two different modes:
- Transport mode:
- Maintain the IP header of the original packet
- Only protects the payload
- Generally used in host-to-host architecture
- Tunnel mode
- Encapsulates the entire packet in another packet
- Generally used in gateway-to-gateway or host-to-gateway architectures
Transport Mode ESP
ESP components:
- Header: SPI identifying the SA and sequence numbers
- Trailer: padding, length, and possibly extra padding for enhanced traffic flow confidentiality
- Auth: MAC of encrypted data and ESP header (not required if authenticated-encryption mode used)
----------------------------------------------------------
| IP header | ESP header | Data | ESP trailer | ESP Auth |
-------------------------|--------------------|-----------
| encrypted |
| authenticated |
Outbound packet processing:
- Original IP data and ESP trailer encrypted with symmetric cipher
- Padding added in ESP trailer
- If SA using authentication service, MAC calculated for ESP header, data and ESP trailer, and appended to the end of the packet (ESP auth)
- i.e. encrypt-then-MAC
- IP header updated
- Protocol field updated to ESP
- Total length field updated
- Checksums recalculated
Tunnel Mode ESP
--------------------------------------------------------------------------
| New IP header | ESP header | IP header | Data | ESP trailer | ESP Auth |
--------------------------------------------------------------|-----------
| encrypted |
| authenticated |
Outbound packet processing:
- Entire packet, along with ESP trailer, encrypted
- If authentication service being used by SA, MAC calculated for ESP header + encrypted section and appended to the end (ESP auth)
- i.e. encrypt-then-MAC
- New outer IP header prepended
- Inner packet contains ultimate source/destination address
- Destination address of outer packet may be different (e.g. may be to a security gateway)
- Set to an ESP protocol packet
Security
- Active attacks exist only for the encryption-only mode of ESP; encryption without integrity known to be insecure
- Attacks due to MAC-then-encrypt configuration
- AH: encryption after MAC
- ESP: encryption before MAC
Virtual Private Networks
Secure channel over insecure connection.
Types:
- Branch office interconnect (intranet VPN)
- Supplier/business partner access (extranet VPN)
- Remote access
Internet VPN: Branch Office Interconnect
Enterprise | Firewall | Internet | Firewall | Branch |
<---- VPN ----->
- VPN tunnel between router/firewalls of main company and branch office
- AH to authenticate data from tunnel endpoints
- ESP to encrypt data over the internet
- Only routers/firewalls need to support IPsec; transparent to clients
Extranet VPN: Supplier Network
Enterprise | Firewall | Internet | Firewall | Supplier Clients |
<---------- VPN --------->
- Supplier may not be part of the enterprise
- VPN extended to operate between router/firewall of main company and individual parts/clients of the supplier TODO
Remote Access
ISPs can provide VPN services across the un-trusted internet.
16. Email Security
Email Security Requirements
SMTP (Single Message Transfer Protocol, RFC 5321) used to transmit email.
Message user agent (MUA) connects client to a mail system, using POP/IMAP to retrieve mail from message store (MS) and SMTP to send mail to a message submission agent (MSA).
The message handling system (MHS) transfers messages from the MSA to the MS via one or more message transfer agents (MTAs).
Message Transfer ... Message Transfer
Agent (MTA) 1 --------> Agent (MTA) n
^ |
| | (Local SMTP)
| v
Message Submission Mail Delivery
Agent (MSA) Agent (MDA)
^ |
| Message Handling |
| System (MHS) |
- - - - - - - - - - - - - - - - - - - - - - - - - - -
| | (Local SMTP)
| v
| Message
| Store (MS)
| |
| | (IMAP/POP)
| v
Message User Message User
Agent (MUA) Agent (MUA)
Email content should be confidential and/or authenticated. The email service should also have a high level of availability.
Spam:
- Unsolicited bulk email (UBE)
- Common vector for phishing
- Email filtering to counter
- Proposal for proof of work: email sender must solve some problem before MHS accepts the email
Link Security
DomainKeys Identified Mail (DKIM)
Domain-to-domain security.
Standard which provides email authentication. RFC 6376.
Sending mail domain signs outgoing emails with its RSA signatures, verified by receiving domain.
Public key of sending domain stored in a DNS record.
Widely used to prevent email spoofing, spam, phishing.
The email contains:
- Version
- Algorithm
- Domain claiming origin
- List of signed header fields
- Hash for those fields
- Hash for the body
- Selector subdividing namespace
- Name of DNS record which contains public key the email was signed with
- e.g. if you want to retire old keys, use different keys for each server
STARTTLS
Extension of SMTP/POP (RFC 2595) and IMAP (RFC 3207) to run over TLS.
Link-by-link security; not end-to-end. However, use of TLS means forwards secrecy may availlable, although this doesn’t help if an attacker controls on of the links.
Link-to-link security allows metadata information (e.g. email destination) to be protected since most nodes provide transmit email for many users (ala VPN), making it hard to determine where a specific email is going from observing network traffic.
Opportunistic use of TLS; use if possible, continue if not available. This makes it vulnerable to STRIPTLS attacks where an attacker interrupts TLS negotiations, making it fail and fall back to plaintext.
End-to-End Security
Client-to-client security.
Pretty Good Privacy (PGP)
Email authentication and encryption for message contents.
- OpenPGP: RFC 4880
- GnuPG: open implementation
Hybrid encryption:
- New random ‘session key’ generated for each new message
- Message content encrypted with symmetric encryption
- Compress plaintext contents with zip
- OpenPGP requires 3DES with 3 keys (168 bits total), recommends AES-128, CAST5 and a few other algorithms to be supported
- Session key encrypted using asymmetric encryption using receiver’s long-term public key
- OpenPGP requires Elgamal support, recommends RSA support
Optional authentication:
- Optionally sign hash of plaintext (SHA1/SHA2) with sender’s private key
- OpenPGP requires RSA signature support, recommends DSA signatures support
- RSA-signed messages hashed with SHA1 (or SHA2)
Then packaging: content encoded with radix-64 so that binary strings can be sent.
Web of Trust:
- Public keys available on distributed key servers
- Users generate their own public/private key pairs:
- Any PGP user can sign another user’s public key, indicating a level of trust
- Users can revoke their own keys by signing a revocation certificate with the revoked key
- Or set an expiry date when generating their keys
Usability:
- Average user can’t understand it
- Difficult to make an interface that allows users to operate PGP correctly and safely
- Vulnerable to EFail
- Client tricked into placing decrypted message within JS or HTML tag, allowing it to be sent to an attacker’s server
Criticisms:
- Old algorithms used
- No support for new ones
- No support for authenticated encryption
- Lots of metadata not protected: file length, recipient key identity
Secure/Multipurpose Internet Mail Extension (S/MIME)
Has similar features to PGP, providing authentication, integrity, non-repudiation and confidentiality of the message body, but it cannot interoperate with PGP.
It includes the sender’s public key in each message, keys being X.509 certificates issued by CAs. It is supported by most popular mail clients.
Authentication:
- Sender:
- Creates message
- Generates message digest
: SHA-256 hash of - SHA guarantee: no one else can find a message
that creates the hash
- SHA guarantee: no one else can find a message
- Signs
with private RSA key to create signature - RSA guarantee: only the owner of the private key can generate
- RSA guarantee: only the owner of the private key can generate
- Sends
and
- Creates message
- Receiver:
- Uses the sender’s public key to verify
- Calculate the digest themselves and check it corresponds to the received digest
- Uses the sender’s public key to verify
Confidentiality:
- Sender:
- Creates message
, random 128 bit content-encryption key for this message - Encrypts
using using AES-128 with CBC mode - Encrypts
using the receiver’s public RSA key - Send
and
- Creates message
- Receiver:
- Decrypts
using their private RSA key - Decrypts the encrypted message using
- Decrypts
The use of symmetric cryptography makes the process more efficient. By using a new ‘session key’ each time (one-time-mechanism), the encryption approach can be strengthened.
17. Malware and Cyber Attacks
Methods
Many different methods to gain access to a target computer:
- Social engineering: persuading an authorized user to do something
- Hacking/cracking: guessing, corrupting or stealing information
- Viruses/worms
- Virus:
- Attaches itself to legitimate programs
- Often causes undesirable behavior
- Automatically spreads to other computers (e.g. through email attachments)
- Worm:
- Runs independently
- Replicates complete copies of itself onto other hosts on a network, often using system vulnerabilities (e.g. WannaCry)
- Virus:
- Trojan horse:
- Harmful piece of software that appears benign and legitimate
- Do not infect files and does not necessarily self-propagate
- Gives attacker remote access to a machine
- Network can be scanned by the attacker’s servers to locate infected machines, forming a botnet:
- Bot: software agent interacting with a service intended for people.
- Botnet: collection of bots running autonomously; usually a collection of compromised machines (e.g. services exposed to the internet using default usernames/passwords) running trojans, worms or backdoors.
- e.g. Zeus:
- Stole bank information through a keylogger
- Spread through drive-by-downloads and phishing attacks
- Network-layer attacks:
- IP spoofing, sequence number predicition, TCP jacking
- Web-based attacks:
- XSS, SQL injection, session hijacking
- Denial of Service (DoS)
- Operating system attacks:
- Ping of death, tear drop, land, snork
- Network attacks:
- SYN flood, TCP fin/rst
- Distributed DoS:
- TCP flood, reflection
- Operating system attacks:
Social Engineering
Persuading an authorized user to disclose sensitive information:
- Inviting user to log into fake website
- Impersonating employee that has forgotten their user ID and/password
- Impersonating technical support staff and requesting that they login to ‘check’ their account
- Persuading a user to install malicious software
Spear phishing:
- Email appearing to be from an individual or business you know
- Attempts to gain access to sensitive information such as credit card/bank account numbers, passwords etc.
Hacking/Cracking
Password discovery: default passwords.
Password cracking tools also readily available for many systems (e.g. zip files, Windows password files).
Password attacks:
- Brute force: all possible permutations of characters
- Dictionary attacks: real-world passwords or permutations of them
- Tools such as L0phtcrack, John the Ripper available
Denial of Service Attacks
Makes network services unavailable to users by overloading servers.
Financial incentive (DOS for hire services) and/or for extortion (stop attack when ransom paid).
No magic solution: use a properly-configured firewall to filter out illegitimate requests, and add more servers.
e.g. TCP SYN-ACK flood:
- Normal SYN-ACK sequence: client asks for connection (SYN), server allocates resources (SYN-ACK), client responds with ACK
- Attack can spoof sender IP address and flood target server with SYN connections; won’t receive response from the server, but forces it to allocate resources for the connection
Rootkits
Collection of programs used to mask intrusion and obtain admin access.
After gaining user-level access to a target system, attacker can install rootkits through known vulnerabilities, password cracking etc.
They may collect user IDs and passwords from other machines on the network. e.g.
Once installed they may:
- Monitor traffic and keystrokes
- Add backdoors
- Alter log files
- Attack other machines on the network
- Alter system tools to circumvent detection
Blended Threats
Combination of attacks using different vulnerabilities:
- Worms dropping viruses
- Destructive trojans horses
- Password stealers
- Remote access trojans (RATs)
- Previously used against energy sectors
- Now aimed at organizations using/making industrial machines/systems
- 2013, Flavex: hacked into websites of manufacturers of industrial control systems and poisoned their software download files
- Trojanized applications that replace system tools
- Multi-platform attacks
- Advanced persistent threats (APTs)
- Stealthy and continuous hacking processes: humans involved in real-time
- Attacking organizations or nation-states
- Requires high degree of covertness over a long period of time
- External command-and-control, continuous monitoring and data extraction
Zero Day Attacks
Taking advantages of software vulnerabilities before the manufacturer can release a patch/fix.
Blaster worm (Windows 2000):
- Extremely virulent
- Optional patch released one month prior to release
Nachi worm:
- Variant of Blaster
- Carried dangerous payload
- Released two days after patch released
Time available to install updates shrinks over time and may be negative in some cases.
Attack Methods
Buffer Overflow
Exploits inadequate buffer boundary checking.
It often involves overwriting return addresses on the stack, making the machine run attacker-controlled code. However, it could also leak memory contents to the attacker.
Heartbleed was an example of the latter:
- https://xkcd.com/1354/
- Bug existed for over two years
- Leaked private keys, user details
- More than 300,000 attacks in a single day
COSC362 Exam Notes
CIA: Confidentiality, Integrity, Availability
Maths
Groups:
- One binary operation
- Four properties:
- Closure:
- Identity: element
such that - Inverse: all elements have inverse
- Associativity:
- Closure:
- Abelian group:
- Additionally commutative:
- Additionally commutative:
- Order:
- of a group: number of elements in a group
- for
in , is smallest integer such that -
generator if ; group cyclic if it has a generator
Finding Generators:
-
- Primes: to find a generator of
: - Use Lagrange theorem; order of any element must exactly divide
- Compute all distinct prime factors
of -
is a generator iff for all
- Use Lagrange theorem; order of any element must exactly divide
- Composite: brute force. Find
, iterate through all values of the group raised to powers up to
Field
- Abelian group for
with identity -
abelian for with identity - Distributivity:
- Finite field: field where operations use modular arithmetic
Chinese Remainder Theorem:
-
Relatively prime
, -
Given integers
and there exists a unique integer such that: -
Solution:
Euler function:
-
: number of integers smaller and relatively prime to -
for prime . -
For integer
with prime divisors : -
Euler’s Theorem: for relatively prime
and :
Fermat Primality Test:
- Uses Fermat’s little theorem: if
for , an are not co-prime and hence cannot be prime - Repeat with multiple values of
(e.g. known small primes); return probable prime if all return - Reduce powers using:
-
- Carmichael numbers: composite numbers that are always found to be probable primes by the Fermat primality test
Miller-Rabin test:
- Only for odd
- Pick odd
and any integer such that - Pick any
- e.g. first 7 primes
- Set
- If
return probable prime - Else repeat the following
times: - If
return probable prime -
- If
- Return composite
Returns probable prime for composite numbers with a maximum probability of 25%.
Discrete logarithm problem:
- Find exponent
that solves - Hard problem: need to brute force values of
Classical Encryption
Confidentiality: reading message requires key.
Authentication: creating message requires key.
Attack classes:
- Ciphertext only: only ciphertexts
- Known plaintext: some plaintexts and corresponding ciphertexts known
- Chosen plaintext: ciphertext of attacker-controlled plaintext known
- Chosen ciphertext: plaintext of some ciphertext chosen by attacker known
Kerckhoff’s Principle: the only thing the attacker doesn’t know is the key.
Systems:
- Transposition
- Message uses permutation
and each block of characters is permuted with this key. If block of length , possible keys - Frequency distribution of cipher/plaintext the same
- Common di/trigrams in the language can be used to optimize trials
- Message uses permutation
- Simple (Monoalphabetic) Substitution Cipher
- Each character replaced with another
- Ceasar: shifted alphabet
-
keys where is the alphabet size - Frequency analysis attacks
- Polyalphabetic Substitution Cipher
-
ciphertext alphabets; th character uses alphabet
-
- Vigenère Cipher
- Polyalphabetic substitution, except that ciphertext alphabets are just shifted alphabets (Caesar)
- Once period identified, substitution tables can be attacked separately
- Autocorrelation: for each possible period length, generate frequency distribution for each alphabet and compare to (shifted) English alphabet frequency distribution
- Kasiski Method: identify sequences of characters the appear multiple times: distance between them likely to be multiple of the period. Find common divisor
- Hill Cipher: Polygram Cipher
- Simple substitution cipher, but substitute multiple characters at a time
- Linear function: multiply each group (column vector) by the key (a matrix)
- Vulnerable to known-plaintext attacks (but may fail if matrix not invertible)
- Ciphertext-only attacks: find probable blocks
Modern Encryption
Hash Functions/MACs
Properties:
- Collision resitance: find collision given no constraints
- Second-preimage resistance: find collision for a given message
- Preimage resistance: can’t find message given its hash
Birthday paradox:
- ~50% chance of finding collision to hash function outputting
bits given trials - ~
trials infeasible today, so hash function outputs should be at least 256 bits - c.f. block cipher key: need
trials for 50% probability of finding key
- ~
Merkle-Damgård Construction:
- Compression function
takes in two -bit inputs and outputs one -bit output - If
collision resistant, whole hash function is collision resistant - Split message into
-bit blocks - Hash IV and first block
- Hash output of above and second block
- …
- Hash output of above and length (plus padding)
- Length extension attacks: hash is full state of the MAC so attacker could add extra blocks
Standards:
- MDx: all broken
- SHA-0/SHA-1: broken
- SHA-2:
- Min 256 bits (i.e. AES-128-level security)
- SHA-512 most secure
- SHA-3: uses sponge function over compression functions
MACs:
- Tag generated from message and secret key
- Unforgeability: cannot produce Message-Tag pair without key
- Unforegability under chosen message attack: above holds even with access to oracle that can calculate MAC for attacker-chosen messages
- But not non-repudiation: signed with session key, not sender’s private key
HMAC:
- MAC from iterated hash function (compression function)
-
- Where
is if is larger than the block size and otherwise - Where
and are known constants
- Where
Encryption and MAC:
- If not using authenticated encryption, there are three options:
- Encrypt-and-MAC: encrypt
, apply MAC to and send ciphertext and tag - Insecure; don’t use
- MAC-then-Encrypt: calculate MAC on
, encrypt , send ciphertext - Encrypt-then-MAC: encrypt
, calculate MAC on , send ciphertext and tag - Most secure but also a bit harder
- Encrypt-and-MAC: encrypt
Block Cipher
Key sizes and equivalents for symmetric algorithms (block ciphers), factoring modulus (e.g. RSA’s
Product cipher: chain simple functions together, each using its own key.
Iterated cipher: product cipher but each round uses the same function using a key derived from a master key (using key schedule).
Substitution-Permutation Network (SPN):
- Substitution/S-box/
: function given sub-blocks of bits and returns substituted bits - Flips some bits; number of
’s in the sub-block will change
- Flips some bits; number of
- Permutation/P-box/
: function given full block and returning a permutation - Number of
’s will not change but the location of them will
- Number of
- In each round, split block into
sub-blocks, run substitution each, then run permutation on the whole block - Round key
XORed with output of previous round, (plaintext for the first round)
Feistel Cipher:
- Split plaintext into left and right
- In each round:
-
-
- Output of (hopefully non-linear) function
XORed, so decryption is same as encryption
-
Shannon:
- Key avalanche: small change in key results in large change to ciphertext
- Relates to Shannon’s notion of confusion: substitution used to make the relationship between
and as complex as possible
- Relates to Shannon’s notion of confusion: substitution used to make the relationship between
- Plaintext avalanche: small change in plaintext results in large change to ciphertext
- Relates to *Shannon’s notion of diffusion: transformations used to dissipate the statistical properties of
across .
- Relates to *Shannon’s notion of diffusion: transformations used to dissipate the statistical properties of
DES:
- 16-round Feistel cipher with 56-bit keys, block length of 64 bits
- Each round uses difference 48-bit subkey
- Plaintext initially permuted with fixed permutation, inverse permutation applied at the end
- Brute-force requires
trials on average - Double encryption: run DES on plaintext, then run DES on the resultant ciphertext with a different key
- Meet-in-the-Middle attack:
- Known plaintext attack
- For a given block:
- Encrypt plaintext with all possible keys; store in memory
- Decrypt ciphertext with any key; compare to above values
- Repeat for all possible keys
- If match found, check if it works for other pairs
- Instead of an average of
attempts, requires storage of ciphertexts, and encryption and decryption operations
- Triple DES:
- Three independent keys approved by NIST; two keys for legacy use; never use one key; can be brute-forced as easily as DES
AES:
- 128-bit data block
- Ceasar: shifted alphabet
- 128, 192 or 256 bit master keys with 10, 12 or 14 rounds respectively
- Byte-based: finite field operations in
- SPN but not Feistel
Block Modes of Operation
ECB (Electronic Code Book):
- Each block uses the same key
-
CBC (Cipher Block Chaining)
- Plaintext XORed with previous ciphertext (or IV)
- Parallel decryption possible
-
CTR (Counter Mode):
- Concatenation of nonce
and block number encrypted - Parallel encryption and decryption
-
Authentication/Integrity
Tag
CBC-MAC:
-
-
is the IV: must be fixed and public - If not, IV must be sent along with the message and attacker has control over
- If not, IV must be sent along with the message and attacker has control over
- The tag is the last ciphertext
CMAC (Cipher-Based MAC):
- NIST version of CBC-MAC
- IV all zeroes
Authenticated Encryption
Data fits into one of two buckets:
- Payload: encrypted and authenticated
- Associated data: only authenticated
This is called AEAD - Authenticated Encryption with Associated Data.
CCM (Counter with CBC-MAC):
If
- CBC-MAC for authentication; CTR mode encryption for payload
- Nonce
(for CTR encryption), payload , associated data - Lengths of
and included in first block; cannot be used for streaming
GCM (Galois Counter Mode):
- CTR mode +
function - Used in TLS 1.2 and 1.3
- TODO more details?
RNGs
Seed obtained from true RNG; used in PRNG/deterministic random bit generator (DRBG).
DRBGs should have:
- Backtracking resistance: access to current state does not allow attacker to distinguish between random noise and previous DRBG output
- Forward prediction resistance: access to current state does not allow attacker to distinguish between random noise and later DRBG output
CTR_DRBG:
- Block cipher in counter mode (e.g. AES)
- ‘Plaintext’ is just zeroes; XOR operation does nothing
- Initialized with seed:
- Seed length = key length + block length
- Seed defines key and counter value (no nonce)
- On each request, return
and increment counter - Maximum of
generate calls before re-seeding
Dual_EC_DRBG:
- Very bad, don’t use, most likely backdoored by NSA
Synchronous Stream Ciphers:
- Both parties must generate the same keystream and be synchronized
- XOR the keystream and plain text to get the ciphertext
- One-Time Pad
- Shannon’s Perfect Secrecy: distribution of messages given ciphertext the same as the distribution of messages
- A5 Cipher, RC4, ChaCha
Public Key Cryptography
One-way function:
- Functions where the inverse is hard to compute
- Integer factorization, discrete logarithm problem believed to be one-way
- Trapdoor one-way functions:
- Inverse easy to compute given additional information - trapdoor
- Asymmetric cryptography: trapdoor is the decryption key
RSA:
- Choose distinct primes
, - At least 1024 bits
-
- Shor’s theorem: polynomial time factorization for
with quantum computers
- Shor’s theorem: polynomial time factorization for
- Choose
such that and are co-prime - Random gives best security
- Small values faster
-
has security issues, prefer larger values (e.g. ) -
should be at least
- Compute
- Public key
- Private key
- Encryption:
- Decryption:
- CRT can be used to increase decryption speed
- Padding required to add randomness
- Håstad’s Attack: if same
and used by different people (i.e. different ), CRT can be used to find in the ordinary numbers and take the th root to find
- Håstad’s Attack: if same
Diffie-Hellman:
- Prime
- Generator
in -
, sent by Alice and Bob respectively - Key
- Relies on discrete logarithm problem being hard
Authenticated Diffie-Hellman:
- Alice sends
and identity - Bob sends
, identity and uses public key to sign , , , and - Alice and uses public key to sign
, , , and - Both compute
Static Diffie Hellman:
Elgamal Cryptosystem:
- Key generation:
- Pick
, generator - Pick long-term private key
-
- Long-term public key
- Pick
- Encryption:
- Pick ephemeral private key
- Send
- Pick ephemeral private key
- Decryption:
-
Digital Signatures
Unforgeability: infeasible to generate a valid signature for any message without key.
Provides non-repudiation.
RSA signatures:
- Signing:
where is a fixed, public hash function - Verification: check that
DSA signatures:
- Elgamal:
- Private key
, public key - Signing:
- Pick
smaller than and co-prime to -
- Find
in - Output
- Ciphertexts twice the size of RSA given same size for
and
- Pick
- Verification:
- Check
- Check
- Private key
- DSA
-
such that has small prime divisor - Generator
in - Generator
- Order
- All exponents can be reduced modulo
prior to exponentiation
- Order
- Signing:
-
- Verification:
-
-
-
- Check
-
- DSA signatures shorter than RSA signatures
-
- ECDSA:
-
order of elliptic curve group - Multiplication modulo
replaced with elliptic curve group operation - Public keys shorter c.f. DSA but signatures are not
- Takes longer to verify c.f. RSA
- c.f. AES, ~double key size
-
Public Key Infrastructure
Trusted certification authority (CA) (CA public key required by clients) issues/signs and revokes certificates.
Certificates (e.g. X.509 v3) contain:
- Public key
- Owner identity
- Signature on the above signed by the CA
- Metadata (e.g. validity period, algorithms)
Usually signed with RSA since RSA verification is faster than ECDSA.
Revocation: each CA has list of revoked certificates.
Key Management
Key management phases:
- Generation (all keys equally likely)
- Distribution
- Protection (only accessible to authorized parties)
- Destruction
Mutual vs unilateral authentication:
- Mutual: both parties authenticate the other party
- Unilateral: only one party authenticates (e.g. client authenticates server)
Pre-Shared Keys:
- Trusted authority (TA) generates and distributes long-term keys to all users when joining
- Only involved during pre-distribution
- Simple scheme: one key for each pair of users -
keys - Probabilistic schemes: high probability of secure channel between any two users
With symmetric keys:
- User and TA share long-term keys
- TA distributes session keys to users when requested
- Fixed Needham-Schroeder protocol:
-
asks for connection with -
sends ID and nonce to -
sends ID and nonce for both parties to TA -
generates session key between and encrypted with long-term key -
sends portion of message encrypted with long-term key
-
With asymmetric keys:
- Each user has public key signed by trusted CA
- Users trusted to generate good session keys; parties must all have good PRNGs
- Session keys encrypted with public keys
- If long-term key compromised, attacker can act as owner
- Forwards secrecy: if compromise does not reveal previous session keys
- Diffie-Hellman: both parties provide input to key material, allowing forwards secrecy
TLS
MAC:
- SHA-2 (>= TLS 1.2)
- MD5, SHA-1 (< TLS 1.3)
Encryption:
- Block cipher in CBC mode or stream cipher
- Most commonly AES. 3DES, RC4 also available (< TLS 1.3)
- Block ciphers: padding applied after MAC to get complete blocks
- Plaintext optionally compressed (< TLS 1.3)
Authenticated-Encryption:
- TLS 1.3: AES with CCM or GCM
- One key for both encryption and MAC
- Header data, (implicit) sequence number authenticated
- Otherwise, uses MAC-then-encrypt by default. MAC
Protocols:
- Handshake: establish session keys
- Record: sends data with established session keys
- Change Cipher Spec (< 1.3)
- Alert
- Warning
- Close notify (sender will not send further messages)
- Fatal
DH Handshake:
- Client hello: highest available TLS version, available cipher suites, client nonce
- Server hello: server’s public certificate, selected TLS version, cipher suite, server nonce
- Server-key exchange: both nonces and DH parameters signed with server certificate
- Client checks signature
- Client-key exchange: client’s DH parameter
- Both parties compute pre-master secret (PMS), then master secret (MS), then session keys
- One key for MAC and encryption for each direction
- IV may also be generated
- Client finished: encrypted with session key
- Server finished: encrypted with session key
RSA: client generates PMS and encrypts with server’s public key. No forwards secrecy.
Anonymous DH: against passive eavesdropping.
Attacks:
- BEAST: CBC mode encryption, allowed byte-by-byte decryption
- CRIME, BREACH: attacker controls part of request, attempts to get it to match cookies or passwords. If request is smaller due to compression, probable partial match
- POODLE: CBC mode encryption, servers would return invalid padding error instead of uniform response.
- Heartbleed: memory contents leaked via bad bounds check
IPSec
Services:
- Confidentiality
- Integrity
- Limited traffic analysis protection
- Conceals IP source, destination addresses
- Message replay protection
- Peer authentication: each endpoint confirms identity of partner
Architectures:
- Gateway-to-gateway
- e.g. connect two secure networks
- No protection between endpoint and gateway
- Host-to-Gateway
- Secure hosts on insecure network
- Each user establishes VPN connection to gateway
- Host-to-Host
- Mostly for special purposes
- End-to-end protection
- All systems need VPN software configured
- Key management system required
Protocols:
- Encapsulating Security Payload (ESP)
- Authentication Header (AH)
- No confidentiality
- Depreciated
- Internet Key Exchange (IKE)
- Managing session keys in Security Associations (SA)
- One SA per direction
- Includes algorithms, keys, security protocol identifier (SA and/or AH)
- IKEv2 used now
- DH with X.509 certificates
- Proof of reachability through cookies: server responds with cookie, client repeats request with cookie
- Cookie can be calculated server-side without requiring server to store any state
- Proof of work: pre-image for partial hash
- Managing session keys in Security Associations (SA)
Modes of operation: ESH/AH operate in:
- Transport: IP header modified, contents protected
- Host-to-host
- IP header modified: protocol changed to ESP, length field modified, checksums
- IP header contains:
- Header
- Packet data and ESP trailer (padding) encrypted
- MAC for header and encrypted data (if SA using authentication service)
- Tunnel mode: original packet encapsulated in new packet
- Gateway-to-gateway or host-to-gateway
- Similar structure, except that encrypted data is the full IP packet, not just the data
Actors and systems:
- Message User Agent (MUA) represents the client
- Message Store (MS) to client: POP/IMAP
- Client to Message Submission Agent (MSA): SMTP
- Message Handling System (MHS):
- System handling email delivery
- MSA -> MS through Message Transfer Agents (MTA)
Link security:
- DomainKeys Identified Mail (DKIM):
- Provides email authentication
- Sending domain signs contents and some headers with public key encryption
- Public key in DNS record
- STARTTLS:
- Link-by-link encryption
- Running IMAP and SMTP/POP over TLS
- Opportunistic: use TLS if available
End-to-end security:
- Pretty Good Privacy (PGP)
- Message encrypted with session key generated for each email
- Session key encrypted with receiver’s long-term public key
- Optional authentication: hash of plaintext signed with sender’s private key
- Web of trust:
- Public keys on distributed servers
- Users sign other user’s public keys, indicating trust
- Revocation: sign revocation certificate with their old key
- Secure/Multipurpose Internet Mail Extension (S/MIME)
- PGP, but with X.509 certificates issued by CAs
- Authentication is required